ILORAZY CZY RÓŻNICE ? (W CHEMII I NIE TYLKO)

Czasem przebieg jakieś zjawiska zależy od dwóch wartości; w wielu zagadnieniach porównuje się dwie liczby. Przy formułowaniu takiej zależności trzeba rozróżniać, jaki zachodzi związek matematyczny pomiędzy wielkościami. Trzeba wyraźnie rozróżniać, czy chodzi o ich sumę, różnicę, iloczyn czy też iloraz. Np. podczas zderzeń cząsteczek istotna jest suma energii kinetycznych dwóch cząstek. Przy badaniu warunków niezbędnych do strącenia osadu jonowego, decyduje o tym iloczyn (potęgowy) stężeń dwóch rodzajów jonów. Przy określaniu stechiometrii istotny jest stosunek (iloraz) liczb moli dwóch reagentów (jest on równy stosunkowi współczynników stechiometrycznych w równaniu reakcji). Na szybkość dyfuzji ma wpływ różnica stężeń substancji w różnych miejscach... Jest to typowy przedmiot scysji podczas kolokwiów studenckich. Studenci coraz częściej zachowują się tak, jakby nie znali znaczenia terminów: suma, różnica, iloczyn, iloraz. Nie tylko zresztą Studenci... Czasem także słyszę: "liczba 9 jest o trzy razy większa od liczby 3". Zatem dla porządku: jeśli się chce określić o ile jedna liczba jest większa od drugiej, to należy od liczby pierwszej odjąć liczbę drugą. Jeśli się chce określić ile razy pierwsza liczba jest większa od drugiej - należy pierwszą liczbę podzielić przez drugą. Tak więc liczba 9 jest trzykrotnie większa od liczby 3, a równocześnie liczba 9 jest większa o 6, od liczby 3. Trochę żenujące jest to wyjaśnianie, ale z roku na rok jest coraz bardziej niezbędne. Kiedyś uczono (i egzekwowano) to w szkole podstawowej...

środki ochronne przy wysokiej próżni

Wiele osób pracujących ze zmniejszonym ciśnieniem zwykłej pompki wodnej (ciśnienie ok. 20 mm słupa Hg) nie stosuje żadnych środków zabezpieczających przed skutkami ewentualnej implozji. Te same osoby podczas pracy z wysoką próżnią pompy olejowej (ciśnienie 0,001 mm słupa Hg) skwapliwie stosują jednak plastikowe osłony na twarz oraz grube rękawice ochronne! Jest zastanawiające, jak trudne jest przekonanie ich, że zagrożenie implozją jest w obu przypadkach niemal identyczne...

Uzasadnienie: O zagrożeniu decyduje nie ciśnienie (próżnia) wewnątrz naczynia, ale różnica ciśnień po obu stronach ścianek naczynia. Przy doskonałej próżni wewnątrz (ciśnienie 0 mm słupa Hg), różnica ta wyniosłaby więc 760 mm słupa Hg (dawniej 1 Atm), co daje nacisk 9,8 N (dawniej 1000 G) na 1 cm² powierzchni ścianki. Praktycznie taki sam nacisk istnieje przy pracy z pompą olejową. Podczas pracy z pompką wodną różnica ciśnień wynosi 740 mm słupa Hg (czyli ok. 97 % poprzedniej wartości), co daje nacisk ok. 9,5 N (dawniej 970 G). Różnica jest więc zupełnie nieistotna.

kiedy można pominąć...

Proste nawet rachunki chemiczne prowadzą często do kłopotliwych równań drugiego stopnia. Przykładem niech będzie obliczenie pH 0,1 M roztworu kwasu octowego (K_a= 2 x 10^-5)

Ka= x2 : (0,1 - x)

(1)

Zazwyczaj przyjmuje się, że wartość ubytku "x" jest bardzo mała, co prowadzi do zastąpienia niewygodnego równania (1) przez wygodniejsze równanie:

K_a= x² : 0,1

Jeśli jednak czynnik "x" w wyrażeniu mianownika pominięto, to dlaczego nie można pominąć tego samego czynnika "x" w liczniku ?

Podczas sumowania lub odejmowania można bez zbytniego błędu mały czynnik pominąć, natomiast nie można zrobić tego w przypadku iloczynu lub ilorazu... Aby to wyraźniej unaocznić, sięgam czasem do następującej analogii. Jeśli na mojej pensji ktoś chciałby dokonać operacji polegającej na dodaniu do niej (lub odjęciu) bardzo małej liczby - mogę się na to ostatecznie zgodzić. Nie będzie jednak dla mnie obojętne, jeśli ktoś chciałby tę wypłatę pomnożyć lub podzielić przez taką samą jak poprzednio małą liczbę!

balony...

Podobny jak przy porównywaniu zagrożenia próżnią, problem rachunkowy pojawia się przy porównaniu siły nośnej balonu napełnionego helem i wypełnionego wodorem. Ponieważ masa molowa helu jest dwukrotnie większa od masy molowej wodoru, wydawać by się mogło, że balon taki powinien mieć dwukrotnie mniejszą siłę nośną. Z prawa Archimedesa wynika jednak, że wypór jest wprost proporcjonalny do różnicy pomiędzy masą^# balonu wypełnionego gazem i masą^# wypartego powietrza. Dla balonu o objętości 22,4 l, w warunkach normalnych, przyjmując średnią masę cząsteczkową powietrza, jako równą 29 oraz pomijając masę powłoki:

wypór przy wypełnieniu wodorem:

(29 g - 2 g) : 1000 * 9,81 m/s² = 0,265 N

wypór przy wypełnieniu helem:

(29 g - 4g) : 1000 * 9,81 m/s² = 0,245 N

W przypadku helu siła nośna balonu jest więc zaledwie o ok. 8 % mniejsza, niż dla balonu wypełnionego wodorem !

^# Zupełnie poprawnie, wypór jest proporcjonalny do różnicy ciężarów, a te są proporcjonalne do mas. Całe rozważanie ma jednak sens tylko w polu grawitacyjnym. W stanie nieważkości wypór równy jest zero.

wyścigi... (“biednemu rowerzyście wiatr zawsze wieje w oczy”)

O tym, jak mylące może być pierwsze wrażenie przy tego typu kalkulacjach, niech świadczy przykład z zupełnie innej dziedziny. Przy próbach ustanawiania rekordów szybkości pojazdów dla uwzględnienia wpływu wiatru przejazd wykonuje się dwukrotnie (tam i z powrotem), a z obu pomiarów czasu oblicza się średnią. Należy jednak uwzględnić fakt, że czynnik korzystny (“z wiatrem”) ma mniejszy wpływ na wynik, gdyż działa on przez krótszy czas, niż czynnik niekorzystny podczas jazdy “pod wiatr”. W związku z tym, z obu czasów przejazdów należy obliczać nie średnią arytmetyczną, lecz średnią geometryczną. Przy kierunku wiatru dokładnie z boku, zachodzi składanie wektorów szybkości, a dla skompensowania jego wyniku należy podziałać dodatkową siłą. Podobnie dzieje się przy kierunku wiatru nieco tylko z tyłu. To paradoksalne, lecz rowerzyści mają więc pełne podstawy aby twierdzić, że podczas jazdy przypadkowy wiatr częściej przeszkadza, niż pomaga...

Tu dygresja: rowerzyści są głęboko przekonani, że jeśli jedzie się rowerem po zamkniętej trasie okrężnej, to suma wzniesień jest większa od sumy zjazdów. Ja także mam takie odczucie. Niestety, próby dowiedzenia tego matematycznie, napotykają na jakieś opory. Może ktoś pomoże? W starożytnej Grecji (prawie) udowodniono, że Achilles nie dogoni żółwia. ( http://wiem.onet.pl/wiem/01127b.html ).

fałszywa waga... Jaka “średnia” ?

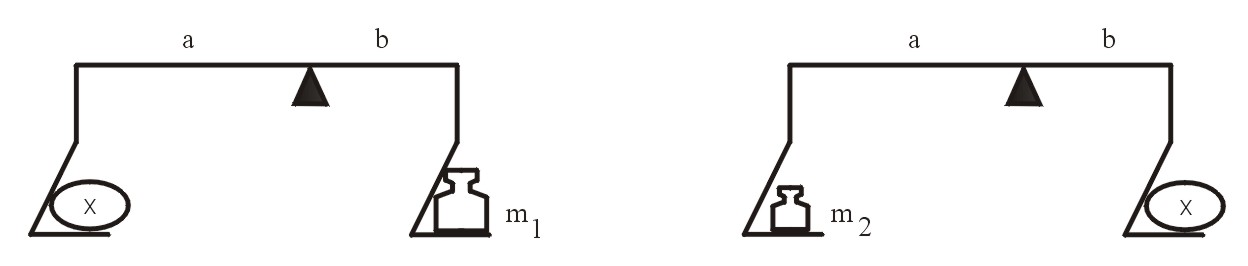
Rzetelna waga powinna mieć oba ramiona o jednakowej długości. Jak dokładnie zważyć nieznaną masę na nierzetelnej wadze, dysponując jednak dobrymi odważnikami? Jedna z metod opisywana w podręcznikach polega na wykonaniu dwóch ważeń, zamieniając stronami przedmiot ważony i odważniki. Z obu pomiarów (m₁, m₂) wyznacza się “średnią”. Podczas ćwiczeń audytoryjnych jedna ze Studentek zwróciła mi uwagę, że powinna to jednak być średnia geometryczna. Istotnie:

a * x * g = b * m₁ * g

a * m₂ * g = b * x * g        (g jest to przyspieszenie ziemskie).

stąd:

x = pierwiastek kwadratowy z: (m₁* m₂)

Na marginesie tych rozważań można zadać pytanie: jak udowodnić, że waga szalkowa służy do pomiaru masy, a nie ciężaru? Należy taką zrównoważoną wagę przenieść (myślowo!) np. na Księżyc. W warunkach zmniejszonej wielokrotnie siły grawitacji, waga pozostanie jednak ciągle w równowadze. Na takiej wadze mierzona jest zatem nie waga (ciężar), ale masa ciał. Paradoksalny jest ten brak konsekwencji ...

Proszę o przeprowadzenie rozumowania, dlaczego waga sprężynowa (tzw. “bezmian”, powszechnie używany np. przez wędkarzy) na Księżycu wykaże inny niż na Ziemi wynik pomiaru (na pewno spowoduje to frustrację wędkarzy księżycowych)?

Z powodów historycznych stosujemy do dziś dawne, niezbyt fortunne nazwy przyrządów, podczas gdy z powodów racjonalnych, dla uniknięcia nieporozumień należałoby chyba dokonać zamiany nazw urządzeń: “waga” na: “masownik” (konsekwentna zamiana terminu “ważenie” na: “masowanie” byłaby jednak zbyt daleko idąca...). Aż dziw, że dotąd nie odkryły tego różne Szacowne Komisje Do Zmieniania Wszystkiego, zazwyczaj aż nadto skłonne do wprowadzania i narzucania zmian...

Oj, skłonni są do ulepszeń... Czasem pytam "ile waży typowa torebka cukru ze sklepu"? Natychmiast pada odpowiedź: 1 kilogram... No, nie... 1 kilogram, to masa takiej typowej torebki; a ja pytałem o wagę (ciężar)! Nieliczne osoby poprawiają się: ok. 9,8 niutona. Czy to nie dziwne: dlaczego taką dziwaczną jednostkę przyjęto? Kiedyś jednostką masy były gramy (kilogramy  g, kg). A jednostkami ciężaru: gramy-siły (kilogramy-siły  G, kG). Gram-siła, to nacisk masy jednego grama na szalkę wagi, na Ziemi, na poziomie morza, na równiku. Bo np. na Księżycu lub w Tatrach, ta sama masa jednego grama, będzie naciskała na szalkę z mniejszą siłą, a więc będzie ważyła mniej. W stanie nieważkości będzie to zerowy nacisk, ciężar takiej masy wyniesie zero; stąd zresztą nazwa "stan nieważkości"... Proste? Najwyraźniej niedopuszczalnie proste, bo Komisja wiele lat temu nakazała zlikwidowanie racjonalnej i życiowej jednostki Gram-siła, i zastąpieniem jej abstrakcyjnymi niutonami. Tak abstrakcyjnymi, że żaden przeciętny człowiek jej nie stosuje, i od tej pory skutecznie nie rozróżnia masy i ciężaru... Czy jajogłowi twórcy tej zmiany przewidzieli takie skutki, i czy są zadowoleni ze stanu zamieszania?

Ponieważ zapis Gram-siła łatwo było pomylić z gramami, zaproponowano inną notację: zamiast Gram-siła, sugerowano zapis: Pond (= Gram-siła).

Średniej z dwóch ważeń nie należy jednak mylić z średnią ważoną (której definicji tu nie podajemy). Nieco wcześniej powoływano się na średnią masę cząsteczkową powietrza. Obliczano ją biorąc pod uwagę udział procentowy składników powietrza. Niedawno zwrócono mi uwagę, że powinien to być jednak ułamek molowy, a nie procent wagowy (75,5% wag. azotu = 78,1 % molowe; 23,1% wagowych tlenu = 20,9 % molowych; 1,3% wagowych argonu = 0,9 % molowe): 0,781 * 28 + 0,209 * 32 + 0,009 * 40 = 28,9. Ponieważ w skład powietrza wchodzą gazy, dla których objętości molowe są identyczne, zatem (paradoksalnie), zamiast procentami (ułamkami) molowymi można posłużyć się procentami objętościowymi !

To nie koniec z językowymi kłopotami. Handlowa nazwa popularnego produktu ”sól warzona” pochodzi od procesu odparowywania wody (wrzątek = ”war”) podczas jego wytwarzania. “Warzelnia soli” zatem nie jest miejscem, gdzie sól się waży, ale zakładem w którym odparowuje się wodę z solanki. Ponieważ produkt jest sprzedawany w postaci paczkowanej, należałoby go określić jako “ważona sól warzona”. Zupełnie podobnie można “nawarzyć piwa”. Wreszcie proces koagulacji (strącania się) koloidów pod wpływem ogrzewania lub dodania niewłaściwego rozpuszczalnika (niezbyt świeże mleko, lakier Nitro rozcieńczany niewłaściwym rozpuszczalnikiem) również określany jest jako “warzenie”. Pan Zagłoba zaś twierdził, że: ”krew żydowska, podlana miodem albo-li winem, warzy się; chłopska, jako leniwa i ciężka, idzie pod spód; a jeno szlachecka animuje się i wyborny tworzy likwor, który ciału daje męstwo i fantazję. Każdej też nacji różne dał Pan Jezus napitki, aby zaś każda miała swoją stateczną pociechę.”

LITERATURA
J.Chem.Educ. 75, 726 (1998). [Siła nośna balonów]

Tomasz Pluciński
nowy adres:  tomasz.plucinski@ug.edu.pl