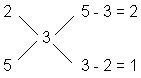
SŁONA ZUPA, LICZBA MOLI SKŁADNIKA, STĘŻENIE MOLOWE SKŁADNIKA

Jednymi z najistotniejszych wielkości chemicznych są: liczba moli składnika oraz stężenie molowe roztworu. Są to jednostki zupełnie różnych wielkości, są one jednak nagminnie mylone przez początkujących chemików. Proponuję, aby grupie takich słuchaczy dać do rozwiązania następujące, bezsensowne w gruncie rzeczy zadanie:

Jakie jest stężenie molowe HCl w 300 ml 2M roztworu kwasu solnego?

Miarą pojęciowego zamieszania będzie powstały spór, czy prawidłową odpowiedzią jest 0,6, czy 2?

Liczba moli składnika (w zapisie: mol) jest jednostką ekstensywną, zależną od wielkości próbki roztworu, natomiast stężenie molowe składnika (w zapisie: M lub lepiej mol/l) jest jednostką intensywną, niezależną od wielkości próbki roztworu. Takie abstrakcyjne rozróżnienie i tak zazwyczaj nie dociera do słuchaczy. Rozsądniejsze jest więc posłużenie się “kuchennym” przykładem ze słoną zupą...

Jeśli próbuje się smak zupy, to jego intensywność (słoność) nie zależy przecież od tego, czy pobiera się kilka kropel zupy, czy też smakuje się ją bezpośrednio z dużego garnka! “Słoność” jest odpowiednikiem stężenia składnika w roztworze i jest ona wielkością intensywną. Natomiast ilość soli, którą spożywa się wraz z zupą (oraz spowodowane tym późniejsze pragnienie) zależy zarówno od tego, jak słona jest zupa, jak i od tego, jak duża była porcja zjedzonej potrawy. Ilość soli jest równa iloczynowi stężenia i ilości roztworu.

typowym przykładem jest propozycja poczęstunku wieczorną kawą. I odpowiedź: „ale proszę nalać dużo wody, bo po mocnej kawie nie mogę zasnąć”. Czyżby następstwa zależały od rozcieńczenia, a nie od ilości brązowego proszku w filiżance? Powinno być oczywiste, że bezsenność zależy od tego ile łyżeczek brązowego proszku wsypano do filiżanki (a następnie do żołądka), a nie od ilości wody! Jeśli zamiast dopełnić filiżankę niewielką tylko ilością wody, a dolać np litr wrzątku, to bezsenność będzie taka sama! Przecież substancją aktywną jest tu kawa, a nie woda! Jeśli opiję się dodatkowo litrem wody, to do bezsenności dołączy się co najwyżej dodatkowe zajęcie w postaci konieczności sikania co godzinę - do rana...

Potocznie używa się określenia "mocna" lub "słaba" kawa (podobnie jak ocet do marynowania grzybków) - jako synonimu "stężony". W chemii ten termin zarezerwowany jest jednak dla pewnej cechy jakościowej klasyfikującej substancje, a związanej z ich dysocjacją. Kwas octowy jest elektrolitem słabym, nawet jeśli sporządzimy 90-procentowy (a więc bardzo "mocny" - a poprawnie: "stężony") jego roztwór.  

Odpowiedź na postawiony problem jest więc następująca: w 300 ml (czyli 0,3 l) 2M roztworu kwasu solnego ilość HCl równa jest 0,6 mola HCl, natomiast w zadaniu pytano o stężenie HCl, które jest oczywiście równe 2M (2 mole/l). Jeśli nie jest to całkiem zrozumiałe, można zrobić odpowiednie obliczenia. Stężenie molowe równe jest liczbie moli składnika podzielonej przez liczbę litrów roztworu:

C_M = 0,6 mola/0,3 l = 2 mole/l = 2M

Wynik ten powinien być oczywisty jeszcze przed wykonaniem obliczeń, jeśli pamięta się o analogii ze słoną zupą. Roztwór 2-molowy ma bowiem stężenie 2M i to przecież niezależnie od ilości tego roztworu!

Do pojęciowego zamieszania przyczynia się dowolność stosowanych oznaczeń jednostek: m, mol, M, ml, m/l, mol/l. Dla uniknięcia niejednoznaczności proponuje się zapis “mol” dla oznaczenia liczby moli składnika, natomiast “M = mol/l” dla oznaczenia stężenia molowego. Jeszcze lepsze, dla uniknięcia śladu niepewności, byłoby pozostawienie pełnego zapisu jednostki stężenia: mol/l.

Niestety, problem znaczenia wielkości intensywnych spotykanych w różnych dziedzinach życia wydaje się być niemożliwy do zrozumienia dla większości niedouczonych dziennikarzy, którzy zamieszanie to potęgują. Nagminne wręcz jest podawanie np. prędkości jednostek pływających w węzłach (oczywiście - morskich!) na godzinę, lub opisywanie ile megawatów mocy wytwarza pewien blok energetyczny w ciągu roku! ^* (Nieodparte skojarzenie z węzłami morskimi na godzinę - to skojarzenie z wężami morskimi!). Szybkość 1 węzła, jest to droga 1 mili morskiej przebyta w ciągu godziny. Węzły na godzinę nie są więc w ogóle jednostką prędkości. Natomiast blok energetyczny pracuje z mocą np. 1000 MW nie tylko w ciągu roku, lecz również w ciągu każdego ułamka sekundy. Moc jest wielkością chwilową i nie zależy od czasu trwania pomiaru - w odróżnieniu od pracy (np. kWh). 

^{*  to trochę tak, jakby posiadacz samochodu chwalił się, że jego silnik ma moc 200 koni mechanicznych (KM) w ciągu miesiąca! Gdybym miał identyczny samochód, odpowiedziałbym mu, że mój ma moc 200 koni w ciągu 1 sekundy...}

Wszystkie tzw. wielkości właściwe (gęstość, czyli masa podzielona przez objętość; szybkość, czyli droga podzielona przez czas; stężenie, czyli ilość składnika podzielona przez ilość mieszaniny; moc, czyli praca podzielona przez czas) są wielkościami intensywnymi. Należą tu również takie cechy jakościowe, jak chociażby barwa (problem smaku i zapachu jest bardziej skomplikowany).

Rozróżnianie pojęć ilości i stężenia jest jednym z elementów zrozumienia chemii, a w szczególności jest ono niezbędne w stechiometrii chemicznej. Zrozumienia tych pojęć nie ułatwiają niestety metody dydaktyczne niektórych nauczycieli chemii. Przykład:

Ile ml (v₂) roztworu o stężeniu 2 mole/l, oraz ile ml (v₅) roztworu o stężeniu 5 moli/l należy zmieszać, aby uzyskać 400 ml roztworu o stężeniu 3 mole/l?

Wielu nauczycieli preferuje użycie graficznego schematu:

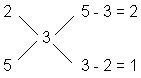
Stąd wynika proporcja zmieszania roztworów: dwie objętości roztworu 2-molowego i jedna objętość roztworu 5-molowego (a skąd wiadomo, że w podanej proporcji należy zmieszać objętości, a nie masy składowych roztworów. A gdyby w zadaniu podane były stężenia objętościowo-masowe?).

Niestety, akceptuje się w ten sposób bezmyślny zwyczaj uczenia się na pamięć niejasnych ^# matematycznych formuł i zaprzepaszcza się pożytki wynikające z racjonalnego myślenia.

^# Aby udowodnić, że powyższy sposób rozwiązania jest rzeczywiście niejasny, proponuję zbadanie, jaki procent audytorium potrafi uzasadnić poprawność powyższego rozwiązania? Stan wiedzy i zdolności intelektualnych znacznego procentu młodzieży określa się coraz częściej jako “zapaść intelektualna”. Wszystko, co wymaga myślenia, a nie daje się obliczyć poprzez automatyczne naciskanie klawiszy kalkulatora, uchodzi za zbyt trudne pojęciowo...

Znalezienie dwóch niewiadomych: (v₂, v₅) wymaga ułożenia układu dwóch równań. Pierwsze równanie jest bilansem objętości roztworów:

v₂ + v₅ = 400

Drugie równanie jest bilansem liczby moli składnika. Z niewiadomych powodów wielu dydaktyków uważa za niewłaściwe korzystanie z proporcji oraz tzw. reguły trzech:

? = v₂ * 2 /1000 moli składnika

Zupełnie podobnie oblicza się liczby moli składnika zawartego w pozostałych roztworach, a następnie układa się równanie bilansowe składnika zawartego w roztworach:

v₂ * 2/1000 + v₅ * 5/1000 = 400 * 3/1000        skąd:        v₂ = ok. 267 ml,    v₅ = ok. 133 ml

Taki sposób rozwiązania preferuje racjonalne myślenie oraz ugruntowuje rozumienie pojęć: “liczba moli składnika” oraz “stężenie molowe roztworu”. Intuicyjne rozróżnianie ich pozwala na uniknięcie wątpliwości podczas praktycznych manipulacji np podczas analizy miareczkowej ("czy w kolbie miarowej przeznaczonej do wydania zadania, może być resztka wody; czy też trzeba kolbę żmudnie suszyć?").  Byłoby pożyteczne wznowienie dyskusji na temat metod rachunkowych w nauczaniu chemii.

Jest rzeczą żenującą, że do takich przykładów muszę się odwoływać wobec absolwentów szkół średnich. Dlaczego jednak nauczyciele w szkole, zamiast starać się o zrozumienie chemii, każą chemii uczyć się na pamięć?

Stężenia mieszanych roztworów są wielkościami nieaddytywnymi (2 M + 5 M ≠ 3 M), w odróżnieniu od addytywnych ilości mieszanych składników (0,533 mola + 0,667 mola = 1,2 mola ). Nie może tego najwyraźniej pojąć rozmówca z anegdoty w przypisie na końcu; czy jednak na pewno rozumieją to moi Studenci?.

P.S. Na grupie dyskusyjnej  pl.sci.chemia  jeden z korespondentów przytoczył  następującą anegdotę:

"... mój znajomy z czerwonym nosem, zaczepił mnie kiedyś na ulicy i z radosną miną i rozpalonym wzrokiem doniósł o swoim odkryciu.
- Wojtek, Wojtek! Ty jesteś chemik, to ty musisz wiedzieć...
- Jasne Jasiek. O co chodzi - spytałem.
- Wiesz. Jak mam jednego jabola, a on ma 18% i wezne drugiego jabola... a on też   ma 18% - przerwał na chwilę, a zmarszczone czoło wskazywało na ogrom wykonywanej, ciężkiej pracy umysłowej, - to jak zleje obie butelki, to powinnem dostać 36% jabola... chyba?
  Tu niepewnie spojrzał na mnie. Co miałem zrobić, jak wytłumaczyć stężenia procentowe, skoro moi studenci nie zawsze to rozumieją. Nagle mnie olśniło! - A jakbyś rozlał jabola do dwóch szklanek, to byś miał w każdej szklance 9% jabola? - zapytałem podchwytliwie.
  Spojrzał na mnie, a w jego wzroku dostrzegłem coś jakby pogardę
- No jasne. Jak wypije jedną szklanke to nic sie nie stanie, a jak dwie, to sie rozochoce na nastepną butelke .. To znaczy, że dwie butelki mają 36% - wrzasnął, ale zawiesił głos i spytał rozglądając się konfidencjonalnie wokoło - Ale jak dasz na jednego bełta to zaraz to sprawdze..."
(Wojtek Szczepankiewicz)

Miły Czytelniku! A jak Ty byś się zabrał do tego beznadziejnego zadania dydaktycznego? (W dodatku za pensję znacznie niższą od średniej krajowej...)

Tomasz Pluciński
nowy adres:  tomasz.plucinski@ug.edu.pl