METODA VSEPR:  PROSTE OKREŚLANIE KSZTAŁTU NIESKOMPLIKOWANYCH CZĄSTECZEK

 

Dlaczego cząsteczki o podobnej budowie: CO₂  NO₂  H₂O mają różny kształt (liniowa, kątowa)?

Teoretyczne przewidzenie kształtu cząsteczek kojarzy się ze skomplikowanym rachunkiem narzędziami chemii kwantowej. Istnieje jednak atrakcyjna z powodu prostoty procedura, wymagająca jedynie podstawowych danych takich jak kolejność atomów w cząsteczce oraz znajomość przynależności pierwiastków do grup układu okresowego. Z naciskiem podkreślam, że nie mają tu zastosowania takie terminy jak liczby kwantowe, orbitale, hybrydyzacja lub mezomeria. Procedura znana jest pod angielskojęzycznym skrótem VSEPR (Valence Shell Electron Pair Repulsion; odpychanie par elektronowych warstwy walencyjnej). Pozwala ona na określenie kształtu cząsteczek (konfiguracji wiązań wokół wybranego atomu leżącego wewnątrz cząsteczki). Daje dobre wyniki: zgodność oszacowanych kątów z dokładnością do kilku stopni z danymi doświadczalnymi - dla atomów pierwszych okresów Układu Mendelejewa. Dla atomów pierwiastków przejściowych procedura jednak często zawodzi.

 

Algorytm przydatny jest dla cząsteczek ponad dwu-atomowych (konfiguracja cząsteczek dwuatomowych jest zawsze taka sama: są one oczywiście liniowe - kłania się tu geometria...). Dla cząsteczek zawierających więcej niż trzy atomy w ciągu szkieletu powtarza się procedurę kolejno dla kolejnych atomów wewnętrznych (dla atomów krańcowych nie ma sensu zastanawianie się nad konfiguracją; wiązanie tego atomu skierowane jest przecież zawsze w kierunku pozostałej części cząsteczki). Zamiast niezręcznego terminu: ligandy (kojarzy się to ze związkami kompleksowymi), proponuję używać określenia podstawniki.

 

Na początku należy zapisać kolejność połączenia atomów cząsteczki, zachowując regułę, że atom tlenu na końcu cząsteczki połączony jest zawsze dwoma wiązaniami (krańcowy atom azotu - trzema); nie należy przejmować się tu dziwacznymi stanami wiązalności atomów wewnątrz cząsteczki. Proponuję prześledzić poszczególne kroki zbiorowo, dla zestawu następujących cząsteczek

 

CO₂    H₂O    O₃    NO₂    HCN    I₃^¯    SO₃    SO₃^2¯    NH₃    NH₄⁺    CH₃COOH

Dla cząsteczki kwasu octowego procedurę trzeba będzie przeprowadzić trzykrotnie, dla każdego atomu wewnątrz cząsteczki osobno, traktując resztę cząsteczki całościowo: H-CH₂-(COOH)   (CH₃)-CO-(OH)    (CH₃CO)-O-H. Ten przypadek proponuję potraktować jako „zadanie domowe”.

 

 

Pierwszym krokiem jest policzenie wszystkich elektronów sfery walencyjnej atomu wokół którego konfigurację ustalamy. Na liczbę tę (N) składają się trzy czynniki:

- elektrony walencyjne tego atomu (równe numerowi grupy układu okresowego: C: 4;  O: 6;  N: 5; I: 7), plus

- elektrony wnoszone przez wiązania oraz

- elektrony związane z ewentualnym ładunkiem jonu (tu pewien problem z rozbudowanymi cząsteczkami: ładunek powinien być zlokalizowany na tym właśnie atomie. Jeśli są wątpliwości - kalkulację lepiej robić dla obojętnej cząsteczki).

Liczbę elektronów wnoszonych przez wiązania oblicza się nieco dziwacznie. Każde wiązanie pojedyncze oznacza wniesienie udziału dodatkowego elektronu. Dla wiązania podwójnego udział wynosi jednak zero; a dla wiązania potrójnego (np do krańcowego atomu azotu w HCN) oznacza deficyt jednego elektronu. O przyczyny takiego rachunku nie należy tutaj pytać: ta nieco irracjonalna procedura jest po prostu skuteczna, i niechaj to wystarczy (chemicy teoretycy pewnie dlatego nie poważają tej procedury)...

Trzecim czynnikiem jest ew. ładunek jonu: dla każdego ładunku anionu wynosi jeden (zsumować jeden elektron), dla obojętnej cząsteczki - zero,  dla pojedynczego ładunku kationu odjąć jeden. Liczba par elektronowych P równa jest N:2. Jeśli liczba par elektronowych jest połówkowa (rzadki przypadek, np dla dwutlenku azotu) to liczbę par zaokrągla się „w górę” (pojedynczy elektron zajmuje tyle samo miejsca co cała para elektronowa).

 

 

 

 

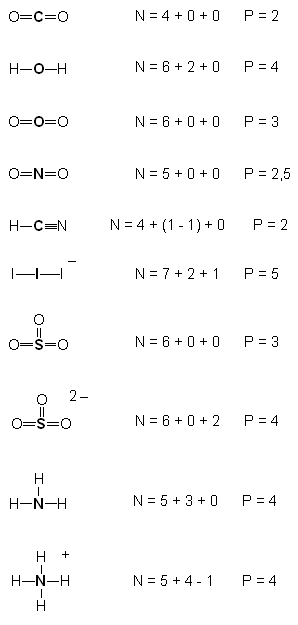
Kolejny krok polega na uruchomieniu wyobraźni geometrycznej. Należy ustalić sposób rozłożenia kierunków w przestrzeni w sposób możliwie najbardziej symetryczny. I tak:

 

P=2

dla P=2 jest to kąt 180 stopni; a więc linia prosta. Tu sytuacja jest już przesądzona: taka cząsteczka (lub ten fragment większej cząsteczki) musi być liniowa!

 

 

 

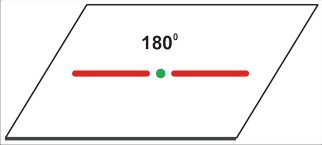
P=3

dla P=3 jest to struktura trzech kątów po 120 stopni - w płaszczyźnie. Cząsteczka (nawet trójatomowa) nie będzie liniowa, ale kątowa (gdy trójatomowa) lub (gdy czteroatomowa) w kształcie gwiazdy [często określa się to niezbyt fortunnie jako "trójkątną". Tu możnaby się zastanowić nad językowym znaczeniem określeń "trójkąt" (trójkątna gwiazda także jest w pewnym sensie trójkątem, bo także ma trzy kąty). Cząsteczki w rodzaju SO₃ mają kształt gwiaździsty, w odróżnieniu od rzeczywiście trójkątnej cząsteczki cyklopropanu (CH₂)₃ ]

 

 

 

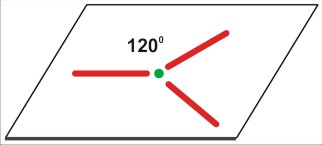
P=4

dla P=4 jest to struktura czterech kierunków ku narożom tetraedru. Takie rozłożenie daje kierunki bardziej odległe od siebie (ok 109 stopni 28 minut), niż w symetrycznej strukturze na płaszczyźnie (90 stopni). Cząsteczka na pewno nie będzie liniowa (nawet trójatomowa), ale kątowa (gdy trójatomowa), w kształcie piramidy (gdy czteroatomowa), lub tetraedryczna (gdy pięcioatomowa).

 

 

 

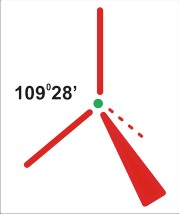
P=5

dla P=5 struktura trzech wiązań po 120 stopni na płaszczyźnie, oraz dwa wiązania ponad i pod płaszczyzną (oba prostopadłe do płaszczyzny). O dziwo, taka cząsteczka trójatomowa może być zarówno liniowa, jak i kątowa (i to z różnymi wartościami kątów).

 

 

 

 

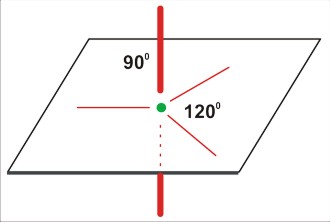
Z naciskiem podkreślam, że na tym etapie struktura (kształt cząsteczki) nie jest jeszcze przesądzona. Opisane twory geometryczne są jedynie podstawą do dalszego etapu modelowania.

 

 

 

 

Zasadniczy krok polega na obsadzeniu podstawnikami wybranych kierunków w przestrzeni: należy uczynić to w sposób nie taki, aby podstawniki były w przestrzeni jak najdalej od siebie ale tak, aby ewentualne nieobsadzone kierunki były jak najdalej od siebie. Tu właśnie popełnia się najczęstsze omyłki! Jeśli podstawników jest tyle samo co kierunków w przestrzeni, to sprawa jest oczywista. Jeśli podstawników jest mniej niż kierunków, należy uruchomić wyobraźnię przestrzenną i dokonać właściwego wyboru. Nieobsadzone przez podstawniki kierunki zajmują wolne pary elektronowe, które silnie się odpychają, "ściskając" kąty pomiędzy wiązaniami.

 

Odrębnym problemem jest nazwanie kształtu cząsteczki.

Dla trójatomowej cząsteczki P=2 [A₂B czyli AB₂  (to przecież tylko kwestia umownej kolejności zapisu, byle tylko był to przypadek P=2) lub ABC:  CO₂ ; HCN]  jest to kształt liniowy; kąt 180 stopni.

                  

 

 

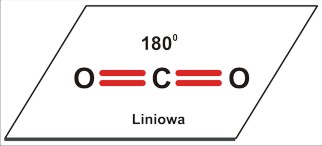
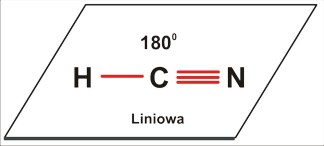
Dla trójatomowej cząsteczki P=3 (O₃ ; NO₂) jest to kształt kątowy (zgięty), płaski, o kącie zbliżonym do 120 stopni (na rysunku nie zaznaczyłem wiązań w cząsteczce ozonu jako podwójne, aby nie drażnić zbytnio zaawansowanych chemików; bez posłużenia się pojęciem mezomerii sensowny zapis wydaje się niemożliwy). Struktura cząsteczki dwutlenku azotu jest podobna.

 

 

 

 

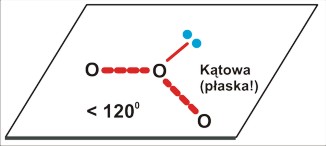
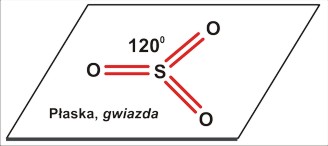
Dla czteroatomowej cząsteczki P=3 (SO₃) struktura płaska z kątami po 120 stopni.

 

 

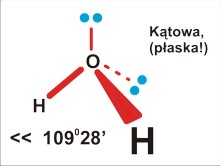
Dla trójatomowej cząsteczki P=4 (H₂O): kątowa, kąt mniejszy od tetraedrycznego (odpychanie podstawników przez wolną parę elektronową zmniejsza kąty wiązań)... Strukturę trzeba także określić jako płaską (sic!, przecież każde trzy punkty leżą na płaszczyźnie. Jest zupełnie inną sprawą, że do tego wniosku doszliśmy analizując rozstawienie podstawników w myślowej strukturze tetraedrycznej).

 

 

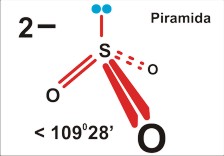
Dla czteroatomowej cząsteczki P=4 (SO₃^2¯ ; NH₃) jest to piramida (trygonalna), kąt nieco mniejszy niż tetraedryczny 109 stopni 28 minut (silne odpychanie podstawników przez wolną parę elektronową zmniejsza kąty wiązań).

 

                    

 

 

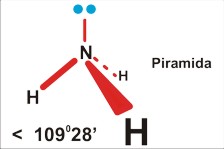
Tu uwaga: chemicy nazywając kształt, biorą niezbyt konsekwentnie pod uwagę jedynie fragmenty zbudowane z atomów, a pomijają wolne pary elektronowe. Dlatego cząsteczkę amoniaku opisują jako piramidę; pomimo, że cała struktura, wraz z wolnymi parami elektronowymi jest tetraedryczna. Wolne pary elektronowe są w tym opisie pomijane... 

 

 

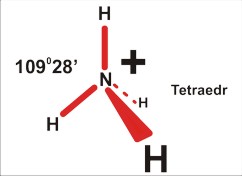
Dla pięcioatomowej cząsteczki P=4 (NH₄⁺) jest to kształt tetraedru: tutaj kąty dokładnie po 109 stopni 28 minut

 

 

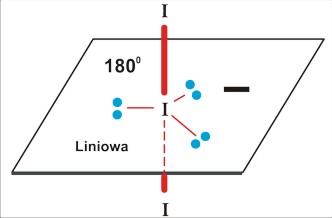
a dla trójatomowej cząsteczki P=5 (I₃^¯) skomplikowane próby rozmieszczenia obu podstawników doprowadzają do wniosku, że struktura tego jonu jest bardzo prosta: liniowa. Komplikacja polega na tym, że o ile dla poprzednich przypadków istniała równocenność w obsadzeniu kierunków mniejszą liczbą podstawników - tutaj trzeba dokonać rzeczywistego wyboru. Dla takiej konfiguracji wolne pary elektronowe są w największej od siebie odległości w przestrzeni (120 stopni), dla wszystkich innych odległość co najmniej dwóch par elektronowych jest mniejsza: 90 stopni.

 

 

Dla porządku przypominam procedurę; obliczenie liczby par elektronowych uruchamia w wyobraźni odpowiedni schemat przestrzenny. Kierunki należy obsadzić podstawnikami pozostawiając w największej od siebie odległości przestrzennej wolne pary elektronowe. Nie sugerując się schematem przestrzennej struktury służącej jedynie celom kalkulacji, nazwać prawidłowo konfigurację wiązań.

LITERATURA
http://pl.wikipedia.org/wiki/VSEPR (całkiem niepotrzebnie wprowadzono tam termin hybrydyzacji)

 

Tomasz Pluciński
nowy adres:  tomasz.plucinski@ug.edu.pl 

F	strona główna

 

   

 

^`