WYPŁYWAJĄCA WODA I MODEL KINETYKI CHEMICZNEJ

**ostatnia aktualizacja: 14.11.2007**

W szkolnych programach fizyki opisywane są jedynie procesy o stałej szybkości, lub procesy o szybkości jednostajnie zmiennej. Rozwiązanie osławionego zadania o wypływającej wodzie

(“opróżnienie 1/10 wanny zajmuje 2 minuty. W ciągu ilu minut opróżni się pół wanny? A ile czasu zajmie opróżnienie całej wanny?” )

bez zastosowania rachunku różniczkowego jest ogromnie uciążliwe. W programach szkolnych nie omawia się niejednostajnie zmiennych zjawisk. Niestety, typowa kinetyka chemiczna jest przykładem takiego właśnie procesu niejednostajnie zmiennego...

Jeśli nawet nie posłużymy się F rachunkiem różniczkowym, to używając jedynie modelu hydraulicznego można uzyskać poprawny obraz zachodzących procesów.

Do eksperymentu należy użyć większej biurety, np. 50 ml i cylindra miarowego. Biuretę napełnić wodą nieco powyżej kreski zerowej i ustalić kurkiem wypływ na ok. 5 ml/minutę. Odczyty objętości dokonywać co minutę i wyniki nanieść na wykres zależności objętości od czasu. Doświadczenie jest bardzo proste, jednak trzeba dokonać odwrócenia oznaczeń na skali biurety. Najwyższej działce (“0”) trzeba dać oznaczenie “50 ml”, kolejnej (“1 ml”) – “49 ml” i.t.d. Dopiero wtedy odczyty będą reprezentować objętość wody pozostałej w biurecie. Jeśli chcemy rzeczywiście wykonać takie doświadczenie, a wyniki mają być dokładne, to na końcówkę biurety należy nasunąć cienki wężyk plastikowy i umocować go syfonowo w statywie tak, aby jego wylot znajdował się dokładnie na wysokości najniższej działki skali biurety.

Woda wypływa z biurety na skutek parcia słupa cieczy. Szybkość wypływu v (można ją określić jako zmianę objętości w czasie), jest proporcjonalna do wysokości słupa wody h:

v = K * h.        K - jest to stała, będąca miarą oporów przepływu.

Jest oczywiste, że szybkość wypływu stale maleje, proporcjonalnie do malejącego z każdą chwilą poziomu wody w biurecie.

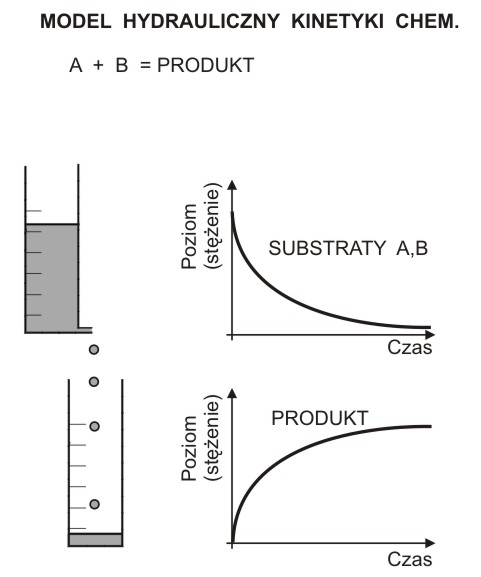
A teraz analogie z kinetyką reakcji chemicznej o ogólnym równaniu:

A + B  →   PRODUKT    (por. s. 55)

Wysokość wody w biurecie (poziom) odpowiada stężeniu substratów A i B, poziom wody w cylindrze odpowiada stężeniu PRODUKTU reakcji chemicznej, a parcie wody odpowiada potencjałowi chemicznemu, proporcjonalnemu do stężeń substratów. Szybkość reakcji (zmiana stężenia reagenta w ciągu sekundy) proporcjonalna jest do (malejącego) stężenia substratów. Równanie kinetyczne może mieć postać:

v = k * [A] * [B].

v - szybkość reakcji
k - stała liczbowa charakterystyczna dla danej reakcji (jest to szybkość reakcji, gdy stężenia wszystkich reagentów równe są jedności)

[A] i [B] - chwilowe stężenia molowe substratów A i B

Szybkość można odczytać z wykresu: jest to tangens nachylenia stycznej do krzywej, w danej chwili. Szybkość reakcji chemicznej jest więc pochodną zmian stężenia reagenta w czasie.

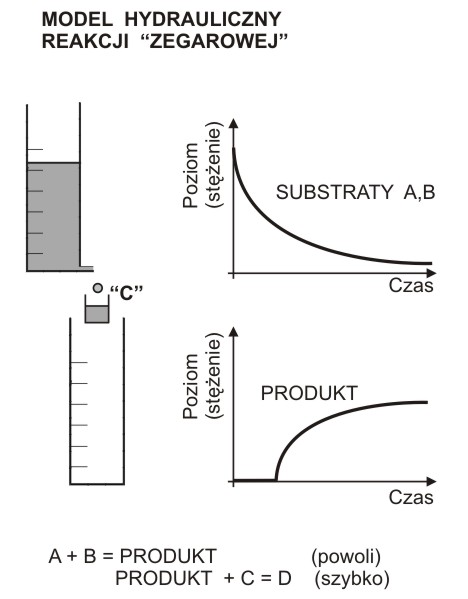
Hydrauliczny model reakcji “zegarowej”

Reakcja “zegarowa” polega na zmieszaniu substratów A, B i C tak dobranych, aby w roztworze zachodziły jednocześnie dwie reakcje:

                    A + B  →   PRODUKT                           (powoli)
                                        PRODUKT + C →   D        (szybko)

(jednocześnie zaś NIE powinny zachodzić reakcje "krzyżowe" A+C lub B+C)

Barwny PRODUKT pojawia się w roztworze dopiero po całkowitym zużyciu substancji C. Po pewnym czasie po zmieszaniu reagentów, roztwór raptownie zmienia barwę.

Można postawić następujący problem: co należałoby zmienić, aby wykres zależności objętości wody zebranej w cylindrze, od czasu, z poprzedniego doświadczenia, był zgodny z krzywą II na rysunku, a nie z krzywą I ?

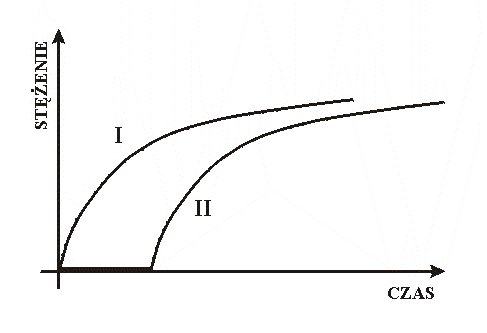
Najprostsze rozwiązanie: pod wylot z kapiącą wodą należy podstawić małe, puste naczynko. Woda w biurecie stanowi odpowiednik substratów A i B, a naczynko symbolizuje substancję C “konsumującą” powstający powoli PRODUKT reakcji A+B. Aby objętość wody w cylindrze zmieniała się zgodnie z krzywą II trzeba, aby woda wyciekająca z biurety była natychmiast gromadzona w naczynku C. Ten warunek jest naturalny w modelu hydraulicznym, nie jest on jednak oczywisty w opisie chemicznej reakcji zegarowej (por. s. 56). Czytelnik sformułuje bez trudu dodatkowy warunek, jakiemu powinna odpowiadać pojemność naczynka C, stanowiąca odpowiednik ilości trzeciego reagenta (“C”) reakcji zegarowej.

No, to przejdźmy jednak do chemicznego opisu rachunkowego...

ZNANE JEST RÓWNANIE:   ZALEŻNOŚĆ SZYBKOŚCI OD CZASU.
JAK WYZNACZYĆ ZALEŻNOŚĆ   STĘŻENIA OD CZASU?
(czyli: JAK OBLICZYĆ STĘŻENIE PO ŻĄDANYM CZASIE REAKCJI?)

Jak przejść od kinetycznego równania różniczkowego (zależność szybkości reakcji od czasu) - do równania całkowego (zależność stężenia substratu od czasu) ?

Należy całkować równanie różniczkowe w przedziale czasu od 0 do „t”. Odpowiada temu przedział zmian stężeń od C₀ do C
 

Reakcja pierwszego rzędu:

„rozdzielenie zmiennych”
pochodną jakiej funkcji jest:  1/C ?
funkcją tą jest:   ln C
[?]’= 1/C       [ln C] ’ = 1/C
całkowanie w granicach zmienności: czasu od 0 do t,    stężenia od C₀ do C

Reakcja drugiego rzędu:

  „rozdzielenie zmiennych”
pochodną jakiej funkcji jest:  C^-2 ?
funkcją tą jest:  -C^-1
[?]’= C^-2       [-C^-1]’ = C^-2:
całkowanie w granicach zmienności: czasu od 0 do t,    stężenia od C₀ do C

Rachunek różniczkowy.
Funkcja pochodna: jak zmienia się nachylenie pierwotnej funkcji (tg kąta nachylenia, czyli tempo zmian funkcji pierwotnej)

Rachunek całkowy.
Funkcja całkowa: jak zmienia się sumaryczne pole powierzchni pod krzywą (czyli np. sumowanie efektów w miarę postępu zmienności)

LITERATURA
J.Chem.Educ. 44, A461 (1967). 54, 557 (1977).
J.Chem.Educ. 74, 1372 (1997). [Skomplikowane modele kinetyki chemicznej]
J.Perelman, “Zajmująca fizyka”, Wyd. Wiedza Powszechna, Warszawa 1955, s. 342. [Zadanie o wypływającej wodzie]

Tomasz Pluciński
nowy adres:  tomasz.plucinski@ug.edu.pl