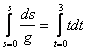RACHUNEK RÓŻNICZKOWY I CAŁKOWY - PO PROSTACKU...
 

Poniższe rozważania na temat rachunku różniczkowego zapewne wzbudzą wesołość wielu dydaktyków. Jeśli zamierzają jednak oni posunąć się do epitetów w stosunku do autora, wyjaśniam, że skłoniła mnie do tego kompletna nieznajomość rachunku różniczkowego i całkowego u maturzystów. W jaki sposób mam realizować program wykładów z opisem kinetyki chemicznej? Epitety (wraz z pozwami przed Trybunał Stanu) należałoby skierować do osób odpowiedzialnych za programy nauczania szkolnego! Chcę przypomnieć, że w latach 60-tych elementy rachunku różniczkowego były elementem programu szkolnego dla wszystkich uczniów. Na czym ma więc polegać postęp intelektualny? Na zrezygnowaniu z matury z matematyki? Powodów, dla którego chemik zdecydował się na zajęcie tematem zarezerwowanym dla matematyków, jest kilka. Po pierwsze: moi koledzy matematycy są tak zafascynowani abstrakcyjnym językiem matematycznym, że nie wyobrażają sobie, aby ktoś mógł mieć jakiekolwiek problemy z tematem. Zdarzyło się kiedyś, że wyłożono studentom („dość daleko spoza profesji”) rachunek różniczkowy. Niestety, zrobiono to w sposób tak hermetyczny, że większość z nieszczęsnych nie zdawała sobie nawet sprawy, że to - o czym była mowa, to był WŁAŚNIE RACHUNEK RÓŻNICZKOWY... 

Czy nie dziwne, że powstała cała dziedzina matematyki, która opisuje sposoby wyznaczania tangensa nachylenia stycznej do danej krzywej? Przy okazji: uczniowie zastanawiają się czasem, czemu tak znaczną uwagę poświęca się w szkole opisywaniu na pozór abstrakcyjnej zależności pomiędzy wartościami kątów i długościami boków trójkąta prostokątnego? Bo trygonometria jest tak ważnym działem (o niezliczonych praktycznych zastosowaniach w nieoczekiwanych dziedzinach), że jej wagi nie można przecenić. Podobnie praktyczna jest możliwość wyznaczenia nachylenia krzywej (a więc po prostu: gwałtowności zmian funkcji). Warto pamiętać, że rzeczywiste procesy w przyrodzie opisywane są najczęściej zależnościami nieliniowymi (tak jak prędkość niejednostajnie zmienna). Zależności nieliniowe opisywane są równaniami w których wykładniki potęg są większe od jedności. Proszę sobie przypomnieć, jakie kłopoty w szkole sprawiał opis ruchu zmiennego (nawet: jednostajnie przyspieszonego) lub opis wypływania wody z wanny pod własnym ciężarem, lub sposób wyznaczania maksimum funkcji lub obliczenie długości obwodu koła... Jaką szybkość ma kulka stalowa wypuszczona z ręki, w 3,7 sekundy po upuszczeniu? Zapewne to niezbyt trudne zadanie potrafią rozwiązać niektórzy Czytelnicy, ale niemal na pewno - zrobią to posługując się wzorem nauczonym na pamięć... Za chwilę okaże się, że rachunek różniczkowy ogromnie upraszcza podobne zadania.

Interpretacją geometryczną rachunku różniczkowego posłużył się w XVII wieku Leibniz, a fizyczną analogią - Newton. Ja posłużę się przykładem doświadczalnego wyznaczenia prędkości pociągu.

Na początku jednak wyjaśnienie pewnego problemu, który sprawił mi swego czasu kłopot: jak zmniejszanie przedziału pomiaru np. czasu, wpływa na wartość ilorazu (ułamka). Np. prędkość jest ilorazem przebytej drogi s do odstępu czasu pomiaru t.    v=Δs/Δt.    Wiele osób intuicyjnie uważa, że zmniejszanie przedziału czasu do zera powoduje, że wartość takiego ułamka także zmierza do zera... 

Na wstępie warto przeprowadzić (myślowo) eksperyment doświadczalnego wyznaczenia prędkości pociągu poruszającego się ze stałą szybkością (załóżmy, że zamierzamy wyznaczyć prędkość dokładnie o godzinie 12.00). Na pół godziny przed wyznaczonym momentem znakujemy (np. pędzlem na szynie) położenie pojazdu, a następnie powtórnie znakujemy położenie w 30 minut po południu: zmierzony odcinek ma 60 km (a więc jest to pomiar drogi w odstępie 1 godziny). Szybkość jakiegokolwiek procesu (chociażby szybkość reakcji chemicznej, tempo inflacji) jest równa stosunkowi zmiany która się dokonała, do przedziału czasu w którym tę zmianę mierzono. Szybkość ruchu (prędkość) równa jest stosunkowi przebytej drogi do czasu mierzenia zmian. W tym przypadku szybkość wynosi więc 60 km/godz. Pomiar można wykonać inaczej: skracając odcinek czasu pomiaru do np. jednej minuty; przebyta droga wyniesie 1000m. Prędkość wyniesie więc 1000 m/min = 60 km/godz. Powinno być oczywiste, że wynik powinien być identyczny jak poprzednio (przecież pociąg jedzie cały czas ze stałą szybkością!).

v = 1000 m/ 1 min. = 60 km/godz    (na rysunku skala nie jest zachowana).

Można oczywiście dowolnie skrócić czas pomiaru, np. do 1 sekundy. Warto sprawdzić, że zmiana położenia wyniesie teraz ok. 16 m 66 cm 7 mm, co po przeliczeniu musi dać oczywiście 60 km/godz. Tak więc długość trwania czasu nie ma wpływu na stosunek przebytej drogi do czasu (prędkość w ruchu jednostajnym). Prędkość jest wielkością intensywną (niezależną od czasu), w odróżnieniu od przebytej drogi.

Proszę sobie teraz wyobrazić podobne zadanie (pomiar prędkości dokładnie w południe), w przypadku pociągu jadącego ze zmienną prędkością (akurat od dłuższej chwili jedzie on z włączonymi hamulcami przed odcinkiem ograniczenia szybkości - wszyscy pasażerowie PKP od lat (!) znają doskonale żółwie tempo od Nasielska do Warszawy...). Wykonanie pomiaru w przedziale 1 godziny dałoby wynik w oczywisty sposób zafałszowany - bo w trakcie trwania pomiaru szybkość zdążyłaby się istotnie zmienić! Wynik pomiaru w przedziale 1 minuty byłby o wiele dokładniejszy... Jeśli chcielibyśmy dokonać pomiaru zupełnie dokładnego, to odcinek czasu powinniśmy skrócić do minimum. Zupełnie poprawnie: rzeczywista (chwilowa) prędkość jest to granica ciągu nieskończonego takiej serii pomiarów, przy czasie trwania pomiaru dążącym do zera. Ten ciąg pomimo to wcale nie dąży do zera; przecież przed chwilą udowodniliśmy, że skrócenie czasu pomiaru nie ma wpływu na wynik pomiaru prędkości ruchu jednostajnego. Granicą skończoną takiego nieskończonego ciągu operacji jest więc rzeczywista chwilowa prędkość. W ruchu niejednostajnie zmiennym taka procedura przybliża wynik do rzeczywistej wartości chwilowej. Ponieważ w miarę zmniejszania przedziału pomiarowego różnice w liczniku i mianowniku ułamka stają się coraz mniejsze - „różnice” stają się więc „maleńkimi różniczkami” - i stąd nazwa rachunku...   v=Δs/Δt  przechodzi w symbol różniczki ds/dt (zapis nie jest zwykłym iloczynem i czyta się go: "de-es po de-te"). Jeśli pytamy jak zmienia się wartość tej różniczki w zależności od zmiennej - to mamy do czynienia z funkcją różniczkową; często stosuje się dla niej notację F’(x) lub po prostu  y’.

Można zapytać o pożytek praktyczny takiej procedury. Zależy on oczywiście od możliwości technicznych oraz możliwości poniesienia kosztów aparatury kontrolnej... Jeśli jednak dany jest wykres zależności przebytej drogi od czasu, to szybkość równa jest tangensowi nachylenia krzywej (właściwie: stycznej) - do osi odciętych (czasu). Podobna procedura ma ogromne znaczenie praktyczne w niezliczonych konkretnych zastosowaniach.

Nieskończony ciąg takich wyrażeń może mieć skończoną granicę... Dla starożytnych Greków był to problem niezbyt dobrze zrozumiały intuicyjnie. Z tego niezrozumienia począł się sławny tzw. F paradoks Zenona (o żółwiu i Achillesie)...

Jako rozrywkę proponuję odczytanie historię pewnej podróży kolejowej, na podstawie wykresu - zapisu przebytej w czasie drogi, z przyrządu analogicznego do tachografu. Pamiętając, że w tym układzie współrzędnych prędkość jest proporcjonalna do (tangensa) nachylenia wykresu.

Pierwszy odcinek odpowiada opóźnieniu odjazdu ze stacji początkowej (na PKP z reguły niemożliwe jest ustalenie przyczyn i winnych takiego spóźnienia; zdaje się, że już wpadam w monomanię w tym narzekaniu na PKP). Kolejne odcinki odpowiadają jeździe z jednostajną prędkością, zatrzymaniem na stacji, kolejnej jeździe ze stałą prędkością (czy taką samą jak poprzednio?), postojowi i powrotowi do stacji początkowej (tangens ma wartość ujemną). Dla uproszczenia pominięto w opisie krótkie odcinki rozpędzania się, czyli jazdy ze zmienną prędkością.

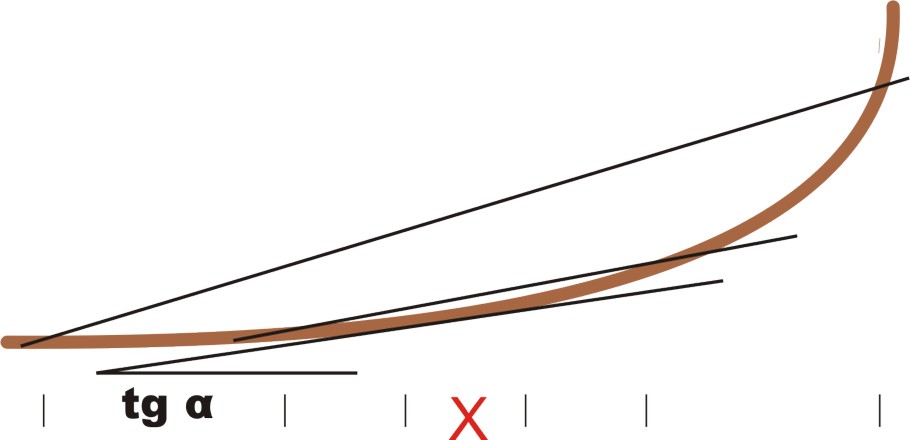
Podsumujmy przebyte rozumowanie dotyczące pomiaru prędkości, w sposób bardziej ogólny, używając terminologii geometrii analitycznej. Jeśli dany jest wykres geometryczny algebraicznego równania opisującego zależność przebytej drogi od czasu, to prędkość w danej chwili jest tangensem kąta nachylenia stycznej do krzywej, w danej chwili.

Jako ilustracja graficzna poniżej: wyznaczenie stycznej w punkcie x, do krzywej - za pomocą ciągu przybliżeń (siecznych) dla zwężających się stopniowo przedziałów zmiennej x

tak ciąg siecznych dąży do stycznej...

Istnieją sposoby dokładnego obliczenia tangensa nachylenia stycznej, w dowolnym momencie - bez dokonywania uciążliwych pomiarów. Tym działem matematyki jest rachunek różniczkowy. Problem sprowadza się do rozwiązania zagadnienia: jeśli dana jest algebraiczna funkcja (zależność): F(x), to jak znaleźć (inną) funkcję, nazywaną funkcją pochodną F’(x) ? Funkcja pochodna ma opisywać zależność (zmienność) tangensa nachylenia kąta stycznej (stycznej do tamtej funkcji pierwotnej).

Sposób w jaki tego dokonano nie na rysunku, ale dla algebraicznych równań funkcji, opisany jest w podręcznikach matematyki; tutaj zadawalam się odesłaniem Czytelnika do tablic, w których można znaleźć zestaw funkcji pochodnych. Tu tylko zwrócę uwagę, że o ile w tablicach logarytmicznych (lub tabelach np. pierwiastków trzeciego stopnia), znajdują się liczby, o tyle w F tablicach różniczkowych znajdują się funkcje algebraiczne (funkcja pochodna, równanie różniczkowe). Najprostsze funkcje pochodne wydedukujemy zaraz bez pomocy tablic. Czytelnik, który zechce uruchomić nieco wyobraźnię i który pamięta, że funkcja pochodna odzwierciedla tangens nachylenia stycznej do funkcji pierwotnej, bez trudu sam dojdzie do wniosku, że dla funkcji:  y = dowolna liczba,  (obrazem jej jest prosta równoległa do osi x), funkcja pochodna równa jest:  y’ = dy/dx = 0. Natomiast pochodną funkcji:  y = ax  jest funkcja  y’ = dy/dx = a (przecież współczynnik kierunkowy w równaniu prostej równy jest tangensowi kąta nachylenia linii na wykresie).

SPADAJĄCA KULKA

Wracając do zadania z kulką: znane jest równanie funkcji przebytej drogi, w ruchu jednostajnie przyspieszonym:    s = gt²/2    (później zostanie to wyprowadzone przy opisie rachunku całkowego).

Prędkość jest pochodną drogi w czasie:   v = ds/dt = g2t/2 = gt = 9,81 m/sek² · 3,7 sek = ...      proste?

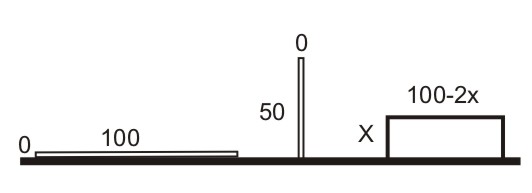
OPTYMALNA DZIAŁKA

Kolejne zadanie: dysponujemy metalowym ogrodzeniem o długości 100m. Należy ogrodzić nim prostokątne pole o największej powierzchni, wykorzystując jako jeden bok prostokąta - istniejącą już w terenie murowaną ścianę. Jaka powinna być długość boku prostokąta?

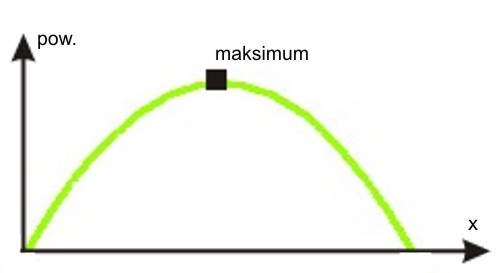
W pierwszej chwili mogłoby się wydawać, że jest to kwadrat...  No, to teraz rachunek różniczkowy. Pole powierzchni równe jest:

s = x (100-2x) = 100x - 2x²  

Obrazem tej zależności nieliniowej jest parabola. Kiedy funkcja ta ma ekstremum? (tu: maksimum; nie wiedzieć czemu w mowie potocznej nadużywa się astronomicznego terminu: apogeum zamiast maksimum...)

Maksimum funkcji to miejsce, gdzie pierwsza pochodna funkcji równa jest zero (styczna jest równoległa do osi odciętych, tangens kąta nachylenia stycznej równy zero). Zatem pierwsza pochodna

 ds/dx = 100 - 4x = 0             stąd:    x = 25 

Największą powierzchnię ogrodzimy płotem o bokach: 25 m; 25 m; 50 m - (oraz ceglana ściana). Powierzchnia ta równa jest  s = 25 m · 50 m = 1250 m²               proste?

Zadanie powyższe można inteligentnie rozwiązywać intuicyjnie zauważając, że dwie sytuacje skrajne dają pole powierzchni równe 0 (na rysunku wyżej są to:  x=0  oraz x=50). A więc rozwiązanie znajduje się gdzieś pośrodku...

No, to jeszcze jedna możliwość. A gdyby jako parametr x oznaczyć długość boku ściany? Dlaczego otrzymuje się dziwaczne rozwiązanie x=50 dla zerowej wartości pierwszej pochodnej? Co precyzyjnie znaczy określenie "ekstremum?" A jak

Jeśli pochodna funkcji jest ciągle zależna od zmiennej - jest to pierwsza pochodna. Ma ona także swoją pochodną (drugą pochodną funkcji pierwotnej). Pierwszą pochodną drogi w czasie - jest prędkość. Pochodną tej pochodnej (a więc drugą pochodną drogi w czasie) - jest przyspieszenie (a przyspieszenie może być w fizyce miarą działającej siły). Trzecia pochodna jest trudniejsza w interpretacji technicznej - "zryw".

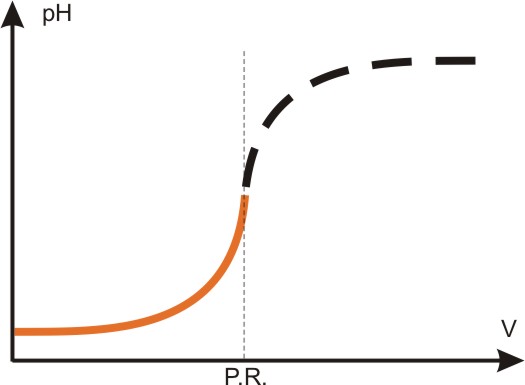
PRAKTYCZNY POŻYTEK Z ANALIZY PRZEBIEGU FUNKCJI MATEMATYCZNYCH, CZYLI: JAK ZBUDOWAĆ AUTOMAT DO MIARECZKOWANIA?

Przebieg zmian np. pH, w miarę dodawania odczynnika miareczkującego (objętość v), podczas klasycznego miareczkowania przedstawia się następująco:

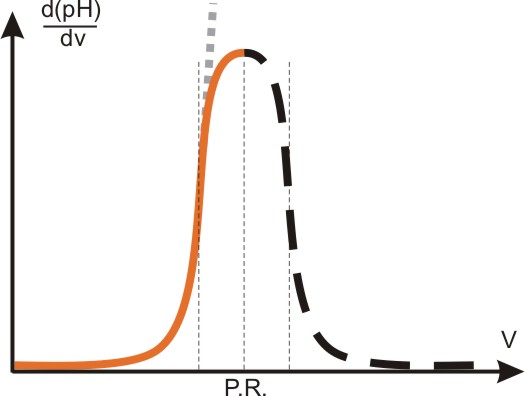
Punkt równoważnikowy P.R. odpowiada zakresowi najgwałtowniejszych zmian, a więc punktowi przegięcia na krzywej. (obraz jest wyidealizowany, bo w rzeczywistości krzywa nie jest zupełnie symetryczna; zmiany po P.R. są mniej gwałtowne).  Zbudowanie przyrządu, który wyłączy w punkcie przegięcia (czyli w P.R.) dozowanie roztworu, nie jest możliwe - bo przyrząd nie potrafi "przewidzieć" czy ten moment właśnie osiągnięto. Wyłączenie możliwe jest dopiero po zauważalnym przekroczeniu tego punktu, a więc ze znacznym błędem dodatnim. W przypadku mało gwałtownych zmian (oraz dużych szumów) błąd ten jest niedopuszczalnie duży.

Jest jednak możliwość rejestrowania nie zmian pH jako funkcji objętości, ale zmian pierwszej pochodnej pH jako funkcji dodanej objętości. Od strony technicznej jest to proste, bo przeliczenia dokonują odpowiednie podzespoły scalone, przy stałej szybkości wstrzykiwania roztworu. Teoretycznie obrazem powinna być krzywa dążąca w P.R. do nieskończoności (przypominam, że w punkcie przegięcia tangens stycznej dąży do bardzo wielkiej wartości; styczna jest prostopadła do osi "v"). Na rysunku jest ona zaznaczona szarą linią przerywaną. W praktyce (szumy, niedoskonała elektronika), krzywa ma kształt dzwonowy.

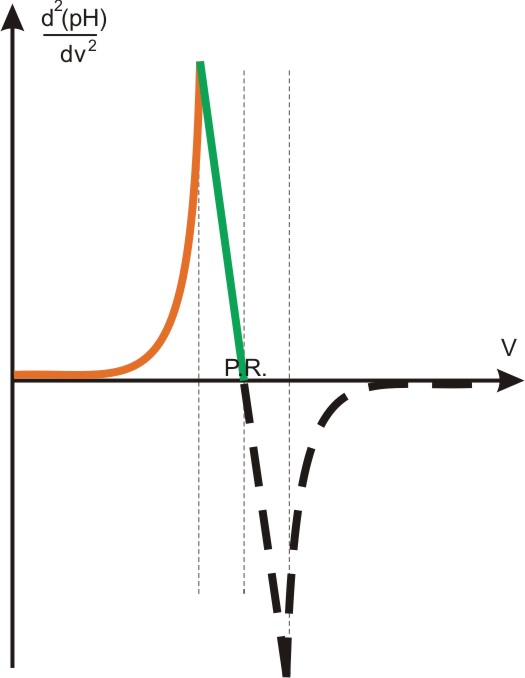
Ta zależność także nie pozwala na zbudowanie automatu (wyłączenie dozowania następuje i tutaj dopiero po istotnym przekroczeniu P.R.).

Rozwiązanie przynosi rejestrowanie drugiej pochodnej zmian pH w funkcji objętości:

Działanie takiego autotitratora przebiega następująco. Po uruchomieniu urządzenia wstrzykiwany jest ze stałą szybkością roztwór miareczkujący, a przyrząd rejestruje drugą pochodną zmian pH. W momencie gdy druga pochodna zaczyna maleć (na rysunku linia pomarańczowa przechodzi w zieloną), otrzymujemy sygnał, że zbliżamy się do PR. W tym momencie następuje zwolnienie tempa (np. 10-krotne) wstrzykiwania roztworu, a gdy wartość drugiej pochodnej zbliża się do zera, przyrząd zostaje wyłączony. Podobnie postępujemy zresztą podczas ręcznego miareczkowania wskaźnikowego: gdy zauważa się pierwsze trwałe ślady zmiany barwy wskaźnika; przykręca się kurek biurety, i ostatnie krople dozowane są już bardzo powoli.

Tu uwaga praktyczna: autotitator nie jest cudownym urządzeniem i nie można nim dokonać miareczkowania niemożliwego do wykonania; w przypadku miareczkowania bardzo rozcieńczonych lub słabych elektrolitów przebieg zmian jest bardzo rozmyty, i szumy elektroniczne powodują jego wyłączenie w dość przypadkowym momencie, dając małą precyzję wyników. Automat daje dobre rezultaty w przypadku takich miareczkowań, które również nie sprawiają kłopotu w tradycyjnej procedurze. 

Jeszcze bardziej fascynujące pomysłowością rozwiązania zastosowano w automatach do miareczkowania kulometrycznego.

W przypadku rzeczywistych pomiarów doświadczalnych (np idea autotitratora; lub odnośnik na końcu do metody Hahna) można więc zastosować procedurę numeryczną, która opisana jest w literaturze. Dla wygody późniejszych obliczeń odstępy pomiarowe powinny być jednakowe, a wielkość przedziału winna zależeć od gwałtowności zmian (im gwałtowniejsza zmienność tym węższy przedział).

Wyznaczanie tangensa nachylenia stycznej na gotowym wykresie - zapisie wyników doświadczenia zostało wcześniej opisane.

Jeśli dysponujemy równaniem algebraicznym, posługujemy się rachunkiem różniczkowym korzystając z tablic funkcji pochodnych oraz reguł rachunku różniczkowego. 

Rachunek różniczkowy daje rozwiązanie problemu równie szybko, co elegancko. Jest więc narzędziem do opisywania rzeczywistych zjawisk (najczęściej niejednostajnych, nieliniowych). Osoby, które tego narzędzia nie znają, są więc w jakimś sensie ułomne w zakresie możliwości opisu otaczającego świata.

 

Niezwykłą właściwością odznacza się funkcja y = e^x ; gdyż  jest ona identyczna ze swoją funkcją pochodną... Stąd zapewne anegdota o nowym pacjencie na oddziale psychiatrycznym, który po krótkim czasie wzbudził tak wielki popłoch, że inni pacjenci chowali się przed nim pod łóżkami. I nie ma się co dziwić, bo nowoprzybyły każdego napotkanego natychmiast różniczkował (ściślej: przekształcał w pochodną - a to przecież żadna przyjemność). Tylko jeden pensjonariusz chodził sobie po oddziale jak gdyby nigdy nic... Na pytanie lekarza dyżurnego o przyczynę pewności siebie, odpowiedział: bo ja jestem „e do iks” !

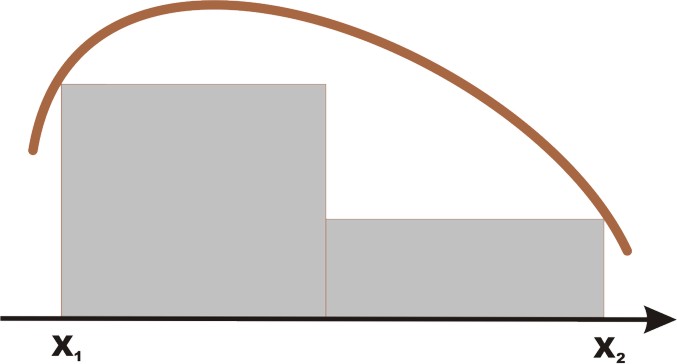
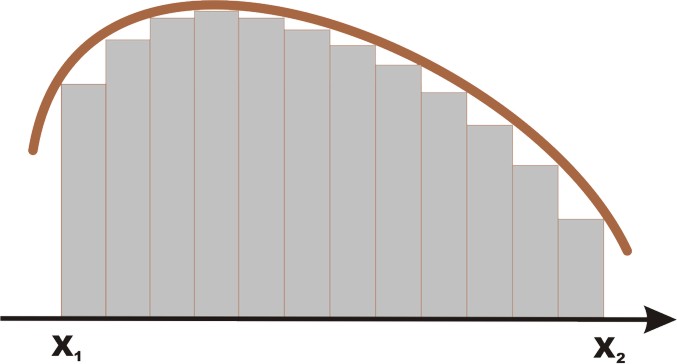
RACHUNEK CAŁKOWY

Jeśli znana jest funkcja pochodna, to funkcję pierwotną można odczytać także z powyższej tabeli. Taka jest procedura obliczania całki nieoznaczonej. Przy interpretacji matematycznej pożyteczniej będzie jednak zrobić to na przykładzie całki oznaczonej (całka nieoznaczona jest funkcją, a całka oznaczona wartością tej funkcji). Niech problem polega na wyznaczeniu ładunku prądu stałego który przepłynął w ciągu pewnego czasu t. Jeśli jest to prąd stały, to w układzie współrzędnych: natężenie-czas, ładunek równy jest polu powierzchni pod wykresem liczonym od czasu x₁ do czasu x₂. Jeśli jednak natężenie prądu zmienia się w czasie, problem się komplikuje. Pole powierzchni należy składać z sumy kilku (najlepiej bardzo wielu bardzo drobnych) prostokątów. Prawdziwa powierzchnia jest granicą takiego ciągu nieskończonego sum coraz drobniejszych prostokątów (coraz dokładniej wypełniających pole pod krzywą).

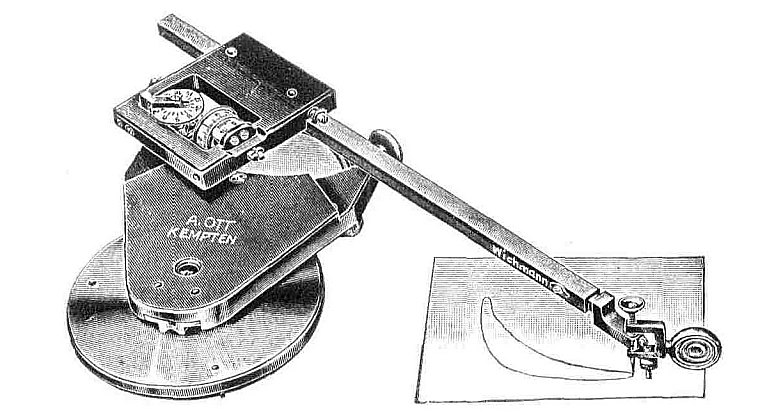
Stąd całkowanie nazywane jest integrowaniem (sumowaniem), a symbolem całki jest zniekształcona i wykrzywiona (dotyczy przecież wielkości zmiennych) stylizowana duża litera „S” - nazywana pieszczotliwie „robaczkiem”.

Wielkościami całkowymi są np. ładunek prądu (w układzie natężenie-czas), przebyta droga (w układzie prędkość-czas), dawka światła (w układzie natężenie światła-czas). Przy okazji o pomiarze światła; w aparacie fotograficznym mierzoną wartością jest natężenie światła (wielkość chwilowa, różniczkowa), a w pomiarach np. agrotechnicznych lub w dozymetrii - dawka promieniowania (wielkość sumaryczna, całkowa). Pomiar wielkości całkowej bywał w dawnych czasach rozbrajająco prymitywny. Np. wartość ładunku prądu zmiennego wyznaczano z wykresu: natężenie/czas, za pomocą mechanicznego urządzenia z ramieniem zakończonym wodzikiem, ze skomplikowanym systemem przekładni - wodząc nim po zapisanym doświadczalnie wykresie i odczytując wartość zakreślonego pola ze skali takiego przyrządu (nazwa: planimetr).

Jeszcze prostszy był wagowy (sic!) pomiar całki. Wycinało się po prostu nożyczkami żądany fragment wykresu, i ważyło go na wadze analitycznej (porównując z wagą kwadratu o znanych wymiarach, wyciętego z identycznego papieru). Skoro mowa o ładunku prądu, genialnie prosty i dokładny jest pomiar wagowy ładunku prądu na podstawie ważenia osadzonego chemicznie produktu elektrolizy (kulometr chemiczny; Prawo Faradaya). Do pomiarów wartości całki używano czasem elektrycznego silnika pomiarowego z mechanicznym licznikiem obrotów (sumatorem). Szybkość obrotów silnika sterowana była napięciem lub natężeniem elektrycznym proporcjonalnym do wielkości mierzonej, a całka była po prostu liczbą dokonanych obrotów - tak jak w mechanicznym liczniku rowerowym! Identycznie zresztą mierzą wartość energii elektrycznej nasze liczniki prądu (obejrzyjcie dokładnie ich funkcjonowanie; mają one element taki sam jak w liczniku rowerowym). Na podobnej zasadzie (ideowej, a nie mechanicznej) oparte są zintegrowane elementy elektroniczne.

przy okazji: irytująco nagminnie mylone są pojęcia mocy i pracy (energii) elektrycznej. Moc (kW, MW) jest wielkością chwilową, intensywną, różniczkową. Praca czyli energia (kilowatogodziny kWh) jest wielkością całkową (sumaryczną), zależną od czasu pracy urządzenia. Rachunki płacimy nie za moc, ale za pracę czyli iloczyn mocy i czasu. Nie są najwyraźniej w stanie pojąć tego niedouczeni dziennikarze, którzy z entuzjazmem opisują ile MW produkuje w ciągu roku (!) blok jakiejś elektrowni... Podobne F problemy mają uczniowie przy rozróżnianiu stężenia molowego i liczby moli w chemii.

Podobnie jak w rachunku różniczkowym, jest możliwość zastosowania (przybliżonej) numerycznej procedury, na podstawie wyników wielu pomiarów wartości podczas trwania zjawiska.

Wszystko to są jednak metody przybliżone. Dokładny pomiar możliwy jest wtedy, gdy znane jest równanie algebraicznej zależności np. od czasu. Przykładem niech będzie wyznaczenie drogi przebytej przez spadające w próżni ciało; zależność wyznaczana w programie szkolnym fizyki w sposób pomysłowy, ale zawiły - a przecież rachunek całkowy daje to rozwiązanie w sposób równie nieskomplikowany, jak elegancki...

Zależność prędkości od czasu jest prosta i intuicyjnie oczywista:  v = ds/dt = g t  (warto zwrócić uwagę, że w tym akurat przykładzie, oczywista jest zależność różniczkowa). Jaką drogę przebędzie ciało od momentu upuszczenia, do końca upływu trzech sekund?

Droga jest całką oznaczoną w przedziale zmiennej od   t=0 do t=3

 ds/dt = g t       

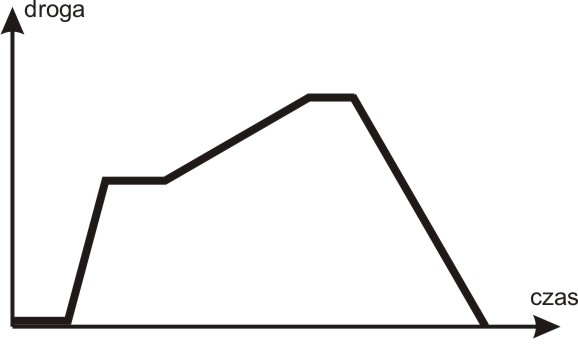
(ponieważ pochodna  t² równa jest  2t, zatem całka po prawej równa jest  t²/2 - bo jej pochodna równa jest t)

s/g = 3²/2        g = 9,81        s = 4,5 · 9,81 = ok. 43 m

Na zakończenie wracam do przykładu odczytania z wykresu historii tamtej pewnej podróży. Tym razem proponuję Czytelnikowi utworzenie wykresu zależności szybkości od czasu (przebyta droga jest polem powierzchni pod krzywą). Wykres ten został umieszczony już wyżej. Suma pól zawartych pod krzywą (przebyta droga) powinna być równa zero (pociąg przebył podróż powrotną).

Zwrócono mi uwagę, że określenie drogi przebytej na trasie zamkniętej - jako zerowej, oraz interpretacja ujemnej wartości pola powierzchni, może być wysoce dyskusyjna. Może w pierwszym diagramie opisującym ruch pociągu zręczniej byłoby umieścić oznaczenie: "odległość" zamiast "droga"? Nie chcę się jednak wdawać w dodatkowe rozważania; niech więc złożone to będzie na karb "prostackiej" formy opracowania...  

Czasem całkowanie nazywane jest operacją odwrotną do różniczkowania. Nie do końca jest to prawdą, bo o ile wynikiem różniczkowania funkcji jest jedna funkcja pochodna, o tyle przy całkowaniu rozwiązań jest nieskończenie wiele (np funkcje 2x;  2x+1; 2x+7 itd. mają tę samą pochodną: 2). O ile w zasadzie daje się obliczyć (w zasadzie) pochodną każdej funkcji, o tyle dokładne rozwiązania funkcji różniczkowych (całkowanie jest przecież operacją na funkcji różniczkowej, zmierzającą do wyznaczenia funkcji pierwotnej) możliwe jest tylko dla funkcji różniczkowych pierwszego stopnia... Pozostałe przypadki dają rozwiązania przybliżone.

KINETYKA CHEMICZNA

Niech przykładem zastosowania rachunku całkowego będzie kinetyka chemiczna. Tu akurat proste i oczywiste - jest równanie różniczkowe opisujące zależność szybkości reakcji chemicznej od stężeń substratów (nazywa się je równaniem kinetycznym reakcji). Jest to równanie eksperymentalne, nie dające się w zasadzie przewidzieć na podstawie równania sumarycznego reakcji. Najczęściej spotyka się dwa typy zależności od stężenia: albo szybkość reakcji jest proporcjonalna do stężenia substratu (przypominam, że skoro stężenie cały czas maleje, to cały proces charakteryzuje się bardzo skomplikowaną nieliniową zmiennością) - albo szybkość reakcji jest proporcjonalna do kwadratu stężenia. Odpowiednio nazywa się te dwa rodzaje zależności: reakcjami pierwszego lub drugiego rzędu. Tym razem chemika może interesować nie jaka będzie szybkość reakcji po pewnym czasie, ale jakie będą stężenia substratów po pewnym czasie.

Jak przejść od kinetycznego równania kinetycznego (zależność szybkości reakcji od czasu) - do równania całkowego (zależność stężenia substratu od czasu)?

Należy całkować równanie różniczkowe w przedziale czasu od 0 (początek reakcji) do „t”. Odpowiada temu przedział zmian stężeń od Co (stężenie początkowe) do C (stężenie po czasie "t").

KINETYKA PIERWSZEGO RZĘDU

v = dc/dt = - k · c       (k -  stała szybkości;  minus - bo stężenia substratów maleją)
„rozdzielenie zmiennych”
pochodną jakiej funkcji jest:  1/c ?       funkcją tą jest:   ln c               [?]’ = 1/c       [ln c]’ = 1/c
całkowanie w granicach zmienności: czas od 0 do t; stężenie od Co do C

KINETYKA DRUGIEGO RZĘDU

v = dc/dt = - k · c²

„rozdzielenie zmiennych”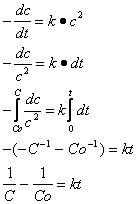
pochodną jakiej funkcji jest:  c^-2 ?       funkcją tą jest:   -c^-1             [?]’ = c^-2         [-c^-1]’ = c^-2
całkowanie w granicach zmienności: czas od 0 do t; stężenie od Co do C

Przy okazji zadanie domowe: jak długo trzeba czekać, aż przereaguje cała ilość substratu? Jaki sens ma więc pojęcie: "czas reakcji"?  A "czas połówkowy reakcji"?  Od czego zależy czas połówkowy w reakcji pierwszego rzędu?  A dla reakcji drugiego rzędu?

I jeszcze jedna uwaga: identyczną postać mają równania opisujące proces wyciekania wody pod własnym ciężarem; dlatego analogii hydraulicznej użyłem w innym miejscu dla zilustrowania jakościowego F opisu kinetyki chemicznej.

LITERATURA

www.geogebra.org/help/geogebraquickstart_pl.pdf
wyznaczanie punktu końcowego miareczkowania metoda Hahna

Tomasz Pluciński
nowy adres:  tomasz.plucinski@ug.edu.pl