LOGARYTMY, SUWAK LOGARYTMICZNY I INNE MASZYNY DO LICZENIA

Powodów dla których chemik zdecydował się na zajęcie tematem zarezerwowanym dla matematyków, jest kilka. Uważam, że należy wykazać, że temat ten nie tylko nie jest trudny, ale może być interesujący; a praktyczne jego zastosowania są wręcz fascynujące (w szczególności dla słuchaczy głośnej muzyki i dla pirotechników). Uzasadniam to szerzej w opracowaniu w odsyłaczu, i ciekaw jestem, czy podzielicie moje zdanie?

Logarytm dziesiętny - to po prostu wykładnik potęgi do której należy podnieść liczbę 10 aby uzyskać liczbę logarytmowaną...

 lg a = x          a = 10^x

po co wynaleziono logarytmy?

Logarytmy są wynalazkiem Napiera (1616 r).

"Wiedząc, że nie ma niczego, co byłoby tak kłopotliwe w praktyce matematycznej, co mnożenie, dzielenie, pierwiastkowanie dużych liczb, - żmudne, czasochłonne, a przy tym często podatne na niebezpieczne błędy - zacząłem w głębi ducha rozważać, za pomocą jakiego sposobu mógłbym usunąć te przeszkody."

Matematyk Briggs specjalnie pojechał do Szkocji, aby poznać Napiera:

"drogi Panie, przedsięwziąłem tę długą podróż po to, by Cię zobaczyć i dowiedzieć się, za jakiego sprytu i dowcipu sprawą pomyślałeś jako pierwszy o tej prześwietnej pomocy dla astronomii... Ciekaw jestem, dlaczego nikt inny nie wpadł na to wcześniej; wszak, gdy się już rzecz pozna, wydaje się taka prosta"

Rozpowszechnienie tablic logarytmicznych wiąże się z rozwojem obserwacji astronomicznych, i kłopotliwością astronomicznych obliczeń. Obliczenia te zajmowały siedemnastowiecznym astronomom ogromnie wiele czasu. http://www.wiw.pl/nowinki/astronomia/200112/logarytmy.asp   Niżej wykażemy, że zastosowanie logarytmów może znacznie ułatwić proste nawet rachunki. W tym opracowaniu zajmuję się jedynie logarytmami przy podstawie 10, czyli logarytmami dziesiętnymi (briggsowskimi).

Kolejne praktyczne zastosowanie logarytmów wiąże się z fizjologią (!). Prawo Webera-Fechnera ma zastosowanie praktyczne dla muzyków oraz pirotechników (a jego nieświadomość może u tych ostatnich skończyć się zdekompletowaniem palców...). Odsyłam tu do F opracowania o pH. Genialne wręcz praktyczne zastosowanie do budowy najprostszej maszyny rachunkowej opiszę nieco dalej. To tylko dzisiejsi uczniowie uważają, że logarytmy wynaleziono dla większego tylko jeszcze udręczenia młodzieży...

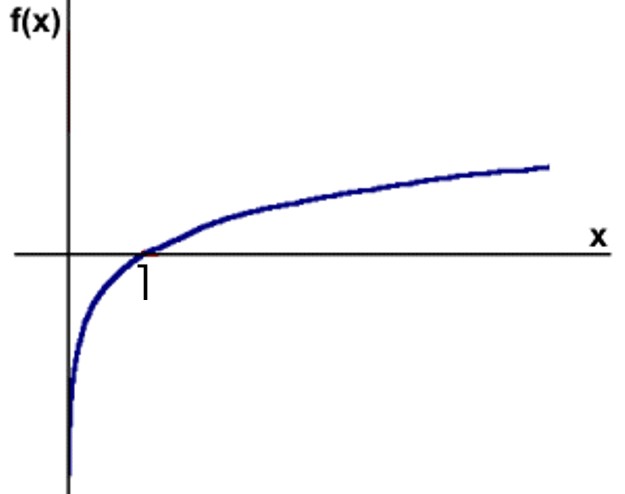
krzywa logarytmiczna i właściwości funkcji logarytmicznej

Zamiast abstrakcyjnych wywodów przytaczam po prostu wykres funkcji logarytmicznej (swoją drogą: mam wrażenie, że w szkołach już przestano uczyć czytania wykresów. O poprawnym rysowaniu wykresów już nawet nie wspominam. A przecież wykres jest najbardziej obrazową formą przedstawiania zależności... Dlaczego to zrobiono uczniom?).

Logarytm - to po prostu wykładnik potęgi, do której podniesiono liczbę 10. Dziesięciokrotna zmiana wartości zmiennej powoduje zmianę wartości jej logarytmu - o jeden... (stukrotna - o dwa; tysiąckrotna - o trzy. Proste?)

No, to zadanie. Są dwa roztwory:  I pH = 2 oraz      II pH = 12.          W którym stężenie kwasu jest większe, i ile razy?           [no, szybciutko: 10 razy (12-2),  czy 6 razy (12:2) ?]

Policzmy...          pH = - lg [H⁺]                [H⁺] = 10^-pH

[H⁺]_I = 10^-2           [H⁺]_II = 10^-12        

[H⁺]_I / [H⁺]_II = 10 000 000 000 razy...

Przecież przed chwilą powiedziano, że zmiana logarytmu (tu: pH) o jedną jednostkę, odpowiada dziesięciokrotnej zmianie liczby logarytmowanej. A zmiana pH o dziesięć jednostek - zmianie stężenia kwasu dziesięć miliardów razy. Pamiętajmy o tym przy czytaniu wykresu miareczkowania alkacymetrycznego...

jak zestawiono tablice logarytmiczne?

Obliczanie logarytmów jest proste jedynie dla liczb będących „okrągłymi potęgami” dziesięciu. Logarytm - to po prostu wykładnik potęgi, do której podniesiono liczbę 10 (a więc: lg 1000 = lg 10³ = 3;   lg10 = lg 10¹ = 1;   lg1 = lg 10⁰ = 0  itd.).   Obliczenie logarytmów innych liczb jest dość żmudne (do znakomitego opisu tworzenia tablic logarytmicznych odsyłam nieco dalej.

Na co dzień mamy do dyspozycji tablice z wartościami logarytmów kolejnych liczb. Teoretycznie tablice logarytmiczne powinny być nieskończenie wielkie (bo każdej liczbie odpowiada jej logarytm, a liczb jest nieskończenie wiele). Zastosowano jednak prosty trick wynikający z właściwości logarytmów. Studenci bardzo nie lubią wprowadzenia pojęcia cechy i mantysy logarytmu; uważają, że są to zbędne komplikacje, skoro jest do dyspozycji kalkulator... Proszę jednak docenić, jak bardzo wynalazek cechy i mantysy uprościł kiedyś konstrukcje tablic logarytmicznych oraz praktyczne zastosowania rachunku logarytmicznego!

Tu wprowadzam pierwsze prawo rachunków z logarytmami:

lg (a  ·  b) = lg a + lg b

Natychmiast wynika z niego, że    lg aⁿ = lg (a  · a  · a  · .... a) = lg a + lg a + lg a + ...... lg a = n lg a     A także:     lg a/b = lg (a  · b^-1) = lg a - lg b.    Każdą liczbę można zapisać w postaci iloczynu potęgowego liczby zawartej pomiędzy 1 a 10, oraz odpowiedniej potęgi liczby 10.

Np. 200 = 2  · 10²        0,2 = 2  · 10^-1    1324 = 1,324  · 10³    

Logarytm każdej liczby składa się więc z sumy (bo logarytm iloczynu jest sumą logarytmów) dwóch części, pierwszej: liczby zawartej pomiędzy 1 a 10 (logarytm ten zawarty jest więc pomiędzy 0 a 1). Ta część nazywana jest mantysą logarytmu; odczytuje się ją z tablic logarytmicznych. Mantysy są zawsze liczbami dodatnimi. Druga część, to logarytm drugiego czynnika iloczynu potęgowego - czyli logarytm potęgi dziesięciu. Jest on równy po prostu wykładnikowi potęgi dziesięciu! Tę część logarytmu nazywa się cechą logarytmu; i jest ona obliczana w pamięci. Np. lg 10² = 2;   lg 10^-1 = -1.            Zatem:

lg 200 = lg (2  · 10²) = lg 2 + lg 10² = 0,3 + 2 = 2,3

lg 0,2 = lg (2  · 10^-1) = lg 2 + lg 10^-1 = 0,3 + (-1) = -0,7

Do obliczenia logarytmów liczb: 2; 20000; 0,02 itp, niezbędna jest jedynie wartość mantysy liczby 2.

Logarytm każdej liczby składa się z części całkowitej, zwanej cechą: jest to całkowita część logarytmu, a wyznaczana jest ona w pamięci. Dla liczb z zakresu 1-10 jest ona równa 0; dla liczb z zakresu 10-100 równa jest 1 itd...

mantysa: ułamkowa, dodatnia część logarytmu, odczytywana z tablicy logarytmicznej. Mantysy liczb np. 2,53   25,3   2530   są identyczne, logarytmy tych liczb różnią się jedynie cechą.

lg 2,53 = 0,40
lg 25,3 = lg (2,53 · 10¹)= 1,40
lg 0,253 = lg (2,53  · 10^-1) = *1,40 = -1 + 0,4 = - 0,6           * nad cechą logarytmu wpisać znak: “minus”
lg 20 = lg (2  · 10¹) = 0,30 + 1 = 1,30
lg 2 = 0,30
lg 0,2 = lg (2  · 10^-1) = -1 + 0,3 = -0,7 = *1,30 ...    

Tak więc tablice logarytmiczne zawierają jedynie logarytmy liczb z zakresu 1 - 10. To, jak są te tablice obszerne - zależy od dokładności tablic. Dla liczb z zakresu 1 - 10 z dokładnością do 1 - jest ich zaledwie 10 (1 2 3 ... 10). Dla dokładności 0,1 jest ich już 100 (1,0  1,1  1,2  ...  9,8  9,9  10,0). Dla dokładności 0,01 jest ich 1000, a dla dokładności 0,001 - aż 10 000. W potocznym zastosowaniu często nie uwzględnia się więc w ogóle przecinka dziesiętnego, a liczby: 0,01324 oraz 132,4 czyta się identycznie: „jeden-trzy-dwa-cztery”.

W powszechnym użytku są tablice logarytmiczne czterocyfrowe.

jak kiedyś obliczono wartości logarytmów „na piechotę”?

Do znakomitego opisu tworzenia tablic logarytmicznych z dowolną dokładnością odsyłam do Wykładów z Fizyki P. Feynmana (Feynmana Wykłady z Fizyki, tomI cz.I, str. 319, PWN, 1971). Podaje on tam kapitalną procedurę obliczania logarytmów, z dowolną dokładnością. W pomysłowy sposób wykorzystano prawidłowości pojawiające się przy operacjach obliczania kolejnych pierwiastków kwadratowych z 10.

przybliżone tablice logarytmiczne do podręcznego użytku...

Proponuję zapamiętanie przybliżonych wartości logarytmów jedynie dwóch liczb:

lg 2 = 0,3010  (ok. 0,3)

lg 3 = 0,4771

Sami łatwo obliczymy stąd, że:

lg 4 = lg 2² = 2 lg 2  = 0,6020

lg 8 = lg 2³ = 3 lg 2  = 0,9030

lg 5 = lg (10 : 2)  = lg 10 - lg2 = 1 - 0,3010  = 0,699 (ok. 0,7)

lg 2,5 = lg (5 : 2)  = 0,699 - 0,301  = 0,398 (ok. 0,4)

lg 1,5 = lg (3 : 2)  = 0,4771 - 0,3010  = 0,1761

lg pierwiastek 2 = lg 2^1/2  = 1/2 lg2  = 0,1505

lg 6 = lg (2  · 3)  = 0,3010 + 0,4771  = 0,7780

lg 16 = lg 4² = 2 lg 4 = 1,2040       [inaczej:  lg 16 = lg (2  ·  8) = 0,3010 + 0,9030 = 1,2040] 

jeśli tak, to:     lg 1,6 = lg (16 : 10) = 1,2040 - 1 = 0,2040

lg 9 = lg 3² = 2  ·  lg 3 = 0,9542

Dla rozrywki (bo dlaczego się nie pobawić logarytmami?) proponuję zadanie: logarytmy (mantysy) jakich innych liczb można jeszcze łatwo obliczyć w podobny sposób?

Do kompletu należałoby może zapamiętać jeszcze jedną wartość: lg 7 = 0,845

Kolejny problem: należy zapisać liczbę: 10^-4,7 w postaci iloczynu potęgowego.
10^-4,7 = 10^(-4-0,7) = 10^{(-4-1-0,7+ 1)} = 10^{(-5 + 0,3)} = 10^-5  · 10^0,3 = 2  · 10^-5

bo: ...10^0,3 = ?, ...   Po zlogarytmowaniu:
0,3 lg 10 = lg ? ...   (lg 10 = 1)
0,3 = lg ? ... ...   logarytm  jakiej  liczby równy jest 0,3 ?
Jest to liczba 2. ...   Zatem: 10^0,3 = 2

 

dodawanie i odejmowanie zamiast mnożenia i dzielenia   

Teraz przykłady praktycznego zastosowania logarytmów do wykonania prostych obliczeń.

Mnożenie 4  ·  5.

Zamiast mnożenia liczb wykonujemy dodawanie logarytmów tych liczb: lg 4 + lg 5 = 0,602 + 0,699 = 1,301. Logarytm jakiej liczby równy jest 1,301? (znajdywanie liczby o danej wartości logarytmu, z łacińska określane było jako Numerus Logarythmi). Jest to liczba z zakresu 10-100 (bo cecha równa 1), a z tablic logarytmów odnajdujemy „Nlog” równe 2 (lg 2 = 0,301). Zatem liczbą tą jest 20 (a nie 2 lub 200). Ta procedura jest bardzo wygodna przy wykonywaniu szeregu wielu kolejnych mnożeń i dzieleń (dzielenie zastępujemy oczywiście odejmowaniem logarytmów). Potęgowanie i pierwiastkowanie omówiono właściwie przedtem, w tym miejscu przypominam, że potęgowanie zastępuje się prostszym od niego - mnożeniem (przez 2 jeśli trzeba obliczyć kwadrat, przez 3 jeśli trzecią potęgę), a bardzo uciążliwe pierwiastkowanie - stosunkowo prostym dzieleniem (na pół jeśli pierwiastek kwadratowy).

[---]  laikowi, który nie chce wiedzieć jak to działa ale co to robi, można dość łatwo powiedzieć prawdę. Nie będzie to cała prawda, ale będzie to prawda dość prawdziwa: otóż łatwiej jest dodawać niż mnożyć. Logarytm to maszynka, co zastępuje zadanie niełatwe zadaniem łatwym. Można myśleć, że logarytm to taka duszyczka liczby (dodatniej) - i że znając duszyczkę da się odszukać liczbę. A więc zamiast przemnożyć dwie liczby sumuje się ich duszyczki, spogląda się na wynik i pyta się: a czyją ty jesteś duszyczką? A duszyczka odpowiada:  jam jest od iloczynu owych liczb.                                                                              http://www.andsol.org/polski/loga.html

mnożenie, dzielenie, potęgowanie i pierwiastkowanie za pomocą linijek: genialny wynalazek suwaka logarytmicznego

Skoro wykonywanie podstawowych działań za pomocą logarytmów jest tak proste - to czy nie możnaby zrezygnować z jakiejkolwiek procedury zapisu na papierze, a zastąpić je mechanicznym manipulowaniem linijkami z naniesionymi skalami logarytmicznymi?

Taka jest idea budowy suwaka logarytmicznego, wynaleziona w 1620 roku przez E. Guntera, a zrealizowana w 1632 roku przez W.Oughtreda. Podstawową częścią suwaka są dwie przesuwne względem siebie linijki z naciętymi identycznymi skalami logarytmicznymi (praktycznie jest to przesuwna linijka w nieruchomym korpusie).

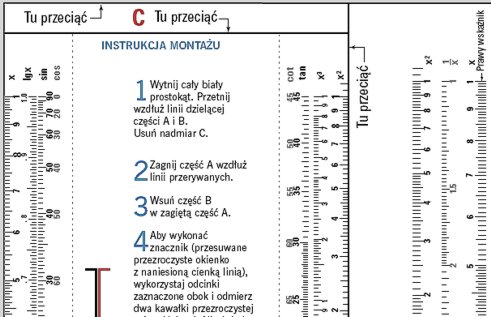
Na zdjęciu widoczne są m.in. identyczne skale podstawowe C (na zielonej przesuwce) i D na korpusie, czerwona skala odwrotności CI oraz przesuwane okienko z rysą nastawczą.

(w cytowanym na końcu artykule w Świecie Nauki jest zamieszczony suwak papierowy do własnoręcznej konstrukcji; tutaj F rysunkowa instrukcja.

 Bardzo polecam zmajstrowanie tego urządzenia; miłej zabawy!

Na rysunku niżej przedstawiono wykonanie mnożenia 3  · 2 za pomocą suwaka (będzie to właściwie dodanie odcinków symbolizujących liczby 3 oraz 2 za pomocą przesuwanych linijek, i odczytania tej sumy). Wynik mnożenia: 6 odczytuje się na dolnej linijce.

Jeśli wynik sumowania nie mieści się na dolnej linijce (a suwak nie zawiera dodatkowej przedłużonej skali w prawo), można górny odcinek odpowiadający mnożnikowi dodawać „w lewo”. Na liczbę mnożnej na dolnej linijce nastawić nie lewą, ale prawą jedynkę (jeśli ktoś woli - to "dziesiątkę") górnej skali, a wynik odczytać pod liczbą mnożnika górnej linijki dodając odcinki „w lewo”. Proszę uwierzyć, że taka procedura jest również dodawaniem a nie, jak możnaby sądzić - odejmowaniem odcinków. Problemu tego nie ma na suwaku kolistym, ponieważ początek i koniec skali łączą się w okrąg właśnie w miejscu jedynki. Na zdjęciu nieco wyżej nastawione jest właśnie mnożenie: 1,05 X 1,4= 1,47 ; lub dzielenie: 1,47 : 1,4 = 1,05

Dzielenie na suwaku jest jeszcze prostsze niż mnożenie! Na wartość dzielnej na dolnej linijce nasuwa się wartość dzielnika na górnej linijce. Wynik dzielenia odczytuje się na dolnej skali pod dowolną jedynką górnej  skali.   8 : 4 = 2.

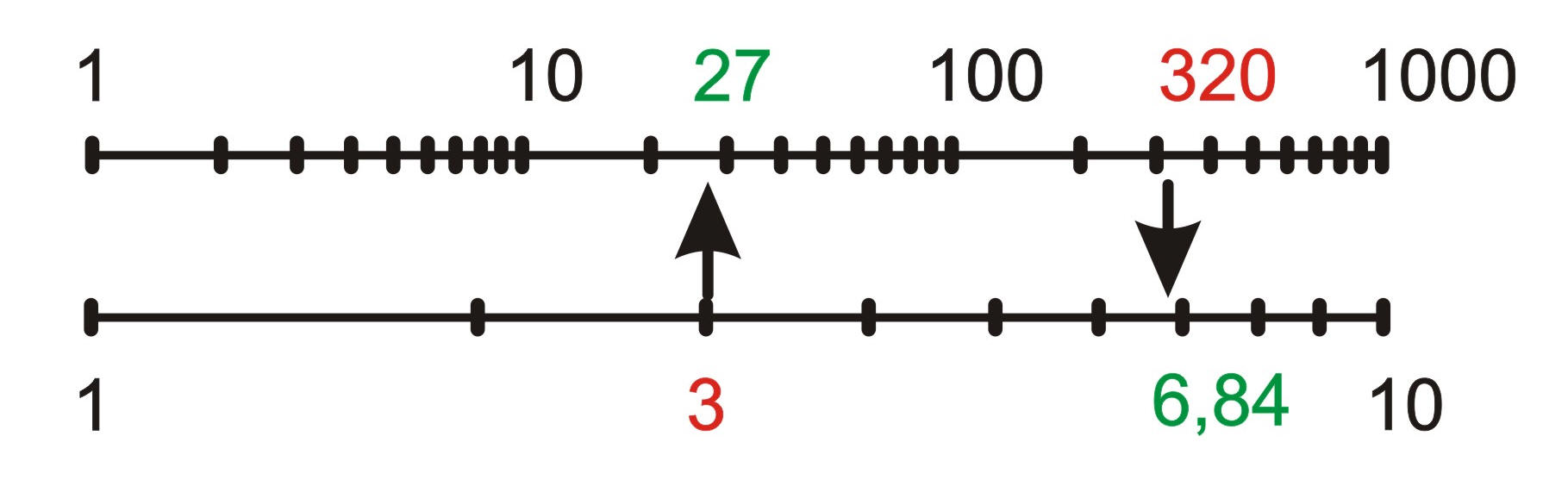
Potęgowanie i pierwiastkowanie na suwaku jest jeszcze prostsze, niż mnożenie i dzielenie, bo w ogóle nie wymaga przesuwania linijek! Przykładem niech będzie odczytywanie sześcianów liczb, oraz pierwiastków trzeciego stopnia. W tym celu nad podstawową skalą logarytmiczną suwaka umieszczone są skale logarytmiczne trzykrotnie „zagęszczone” (a więc mieszczą się takie trzy skale). Jeśli na dolnej skali zaznacza się liczbę, to nad nią, na górnej skali sześcianów odczytuje trzecią potęgę tej liczby. A jeśli liczbę zaznaczyć na górnej „zagęszczonej” skali, to na dolnej skali podstawowej odczytać można natychmiast pierwiastek trzeciego stopnia z tamtej liczby. Niżej podane przykłady, to 3³ = 27 oraz pierwiastek trzeciego stopnia z 320 = 6,84 (trzeba przyzwyczaić się do odczytywania wartości ze skal suwaka).

Do podobnych celów służą skale kwadratów (i pierwiastków drugiego stopnia). Jest to właściwie typowy przykład zastosowania nomogramu. Podobnym nomogramem jest skala 1/x (obliczanie odwrotności liczb). Jest to podstawowa skala logarytmiczna, odwrócona tylko o 180 stopni. Trzeba więc pamiętać, że należy czytać ją od prawej do lewej...

Do wyjaśnienia zasady posługiwania się suwakiem niezbędne jest co prawda rozumienie zasad rachunku z logarytmami, natomiast praktyczne posługiwanie się suwakiem nie wymaga znajomości nawet definicji logarytmu.

Na niektórych suwakach nacięte są dodatkowo skale e^x  e^0,1x oraz e^0,01x . Służą one do obliczania potęg i pierwiastków o dowolnych wykładnikach (również ułamkowych!). Typowy suwak najczęściej zawiera jeszcze pomocnicze skale służące nie tyle do obliczeń, ile stanowiące podręczne tablice liczbowe wartości logarytmów (właściwie: mantys. Paradoksalnie: ta skala jest na suwaku logarytmicznym jedyną skalą równomierną), oraz skale-nomogramy wartości funkcji trygonometrycznych: sin, cos, tg (skali wartości ctg nie ma na suwaku; w tamtych czasach można było jeszcze liczyć na inteligencję użytkownika, który wiedział, że ctg jest równy odwrotności tg kąta... Obawiam się, że dziś wielu Czytelników niezbyt pewnych jest, co oznacza: „dzielna” i „dzielnik”, a funkcje trygonometryczne i logarytmy usunięto z ich programu szkolnego).

Typowy suwak miał długość 25 cm i pozwalał na obliczenia z dokładnością do 0,01. Wyżej zdjęcie fragmentu takiego suwaka firmy VEB MANTISSA. Do celów specjalnych produkowano suwaki dokładniejsze (50 cm), oraz suwaki skrócone (koliste).

Zdjęcie prostego okrągłego suwaka pochodzącego z zaprzyjaźnionej kolekcji (skala podstawowa i kwadratowa)

Wyżej - zdjęcie z eksponatami Pana Wojciecha Sawickiego - ze strony www:  http://www.sawicki.cc/

Rekordem jest suwak, którego skala logarytmiczna o długości 12,5 metra (!) "nawinięta" jest spiralnie na pręt o średnicy paru cm, i wysokości 30 cm (mieści się on w kieszeni); suwak ten daje dokładność pięciu (!) cyfr znaczących.

Dla techników określonych specjalności konstruowano suwaki ze specjalnymi skalami: dla elektrotechników, inżynierów budownictwa, chemików itd. Katalog koncernu Wichmann z lat 40-tych zawiera ofertę F  dziesiątków  różnych suwaków, na 26 stronach. 

Paradoksalnie: na suwaku nie da się wykonać dodawania i odejmowania... Ale do tego celu wynaleziono w zamierzchłych czasach liczydła, a potem arytmometry. O dziwo, za pomocą liczydeł daje się wykonywać zadziwiająco skomplikowane zadania rachunkowe; organizowany jest nawet międzynarodowy konkurs, którego laureaci rozwiązują iście imponujące zadania.

Wspomniałem wcześniej, że na suwaku nie odczytuje się miejsca położenia przecinka dziesiętnego. To utrudnienie nauczyło pokolenie "suwakowców" egzotycznego dziś i powszechnie kwestionowanego nawyku myślenia - pamięciowego kalkulowania przybliżonego wyniku (0,0211 x 4,93   to mniej więcej tyle co   0,02 x 5 czyli ok. 0,1).  SUWAK UCZYŁ MYŚLENIA... Teraz kalkulator UCZY BEZMYŚLNOŚCI: proszę podzielić: 0,3:100 (lub pomnożyć: 30x0,2). 3/4 Studentów sięga do kieszeni po kalkulator...   A operowanie zagęszczającą się skalą mimo woli wzrokowo dodatkowo sugerowało rozumienie problemu błędu odczytu i błędu obliczeń.

Do kompletu przytaczam zdjęcie jeszcze jednego eksponatu: mechanicznego urządzenia liczącego, na korbkę: arytmometru. Działające takie urządzenia spotyka się jeszcze w zabytkowych barach i pubach; czyż nie jest piękne?.

dalej - to krok do Enigmy

i Eniaca...

 

Kolejne częste zastosowanie skali logarytmicznej, to ilustrowanie danych za pomocą skal o bardzo wielkiej rozpiętości, np czasu. Gdyby na równomiernej skali o długości np 10 cm chcąc zobrazować historię Ziemi (przyjmijmy: miliard lat), to na tym wykresie okres najbardziej nam bliski, w którym wydarzyło się niemal wszystko to, co najbardziej interesujące - miałby szerokość mniejszą od grubości włosa! Można jednak przyjąć zasadę nierównomiernej skali logarytmicznej. Dla uproszczenia przyjmijmy, że wykonujemy to w roku 2011... Zaznaczamy go na prawym krańcu skali. Jeden centymetr w lewo będzie punkt obrazujący 2010 (rok w tył; no, to akurat może nie jest do końca konsekwentne, ale za to praktyczne...). Kolejny jeden centymetr w lewo, to 10 lat wstecz (lg10 = 1; rok 2000). Kolejne odcinki centymetrowe w lewo odpowiadają kolejno: 1900 (100 lat, lg100=2); 900 itd W ten sposób odległe okresy, w których z naszego punktu widzenia nie działo się nic zbyt intensywnie, zostają ogromnie ściśnięte, a czasy ostatnich lat z natłokiem wydarzeń - ulegają rozciągnięciu. Na podobnych wykresach powinno być bardzo wyraźnie zaznaczone, że jest to wykres zniekształcony - logarytmiczny, o czym trzeba pamiętać interpretując narysowane na nim dane. Podobnie zniekształconą skalą logarytmiczną jest skala pH (bo właściwie chodzi o skalę stężenia (lub aktywności) jonów wodorowych. I jeśli dodatek jednej kropli podczas miareczkowania powoduje zmianę pH o 3 jednostki, to odpowiada temu aż tysiąckrotna zmiana stężenia kwasu. Niekiedy celowo nanosi się dane doświadczalne nie na oś równomierną, ale np. logarytmiczną (np. w danych kinetyki chemicznej). Wtedy obrazem zależności może być linia prosta, której przedłużenie pozwala na wygodne odczytanie z osi liczbowej ważnych stałych kinetycznych. Wiele dużych firm produkujących materiały biurowe, oferuje bogaty asortyment papierów z nadrukowaną siatką: liniowo-logarytmiczną; logarytmiczno-logarytmiczną; trójkątną, liniowo-kolistą itd 

Czasem eksperyment prowadzi do skomplikowanych zależności matematycznych pomiędzy wielkościami. Np zależność pomiędzy wartością napięcia ogniwa a stężeniem kwasu, intensywnością barwy roztworu a stężeniem barwnika, wrażeniem głośności a energią źródła dźwięku. W takiej sytuacji często decydujemy się na zdefiniowanie nowej jednostki, czasem o oryginalnej formule. Zamiast stężenia kwasu wprowadza się więc ujemny logarytm stężenia kwasu; zamiast stosunku natężeń wiązek światła po przejściu przez roztwór - logarytm tego stosunku; logarytm ze stosunku energii głośnika. Jedynym celem takich zabiegów jest uzyskanie liniowej zależności doświadczalnej. Tymi dziwacznie zdefiniowanymi jednostkami są oczywiście: pH, ekstynkcja i decybele... Często jest to skala logarytmiczna. Tak naprawdę pożytek z podobnego zabiegu jest dyskusyjny, bo łatwo zapomnieć o logarytmicznym lub wykładniczym charakterze nowej jednostki. A za taką nonszalancję domorośli F pirotechnicy mogą zapłacić "wydaniem reszty" w postaci palców z osobna...

Wracając do punktu wyjścia (zarzutów, że logarytmy wymyślono sztucznie, dla udręczenia uczniów): myślę, że logarytmiczne zależności "wymyśliła" sama przyroda i natura zjawisk. A ich wprowadzenie do opisu zależności prowadzi do uproszczenia języka i jest tylko dostosowaniem się do faktów. A dodatkowe zastosowania takie jak np. suwak logarytmiczny - są jedynie "bonusem" i nagrodą za ową pokorę.

posłowie...

Powodów, dla którego chemik zdecydował się na zajęcie tematem zarezerwowanym dla matematyków, jest kilka. Po pierwsze: moi koledzy matematycy są tak zafascynowani abstrakcyjnym językiem matematycznym, że nie wyobrażają sobie, aby ktoś mógł mieć jakiekolwiek problemy z tematem. Zdarzyło się kiedyś, że wyłożono studentom („dość daleko spoza profesji”) rachunek różniczkowy. Niestety, zrobiono to w sposób tak hermetyczny, że większość z nieszczęsnych nie zdawała sobie nawet sprawy, że to - o czym była mowa, to był WŁAŚNIE RACHUNEK RÓŻNICZKOWY...  Dajcie więc szansę człowiekowi „spoza fachu”... (I proszę się nie naśmiewać z naiwności powyższego tłumaczenia).

Drugim powodem była skandaliczna tendencja do stopniowego ograniczania wiedzy matematycznej uczonej w szkołach. Z wielu programów szkolnych usunięto logarytmy, trygonometrię... Jak więc w szkołach uczyć jednostki pH? A jak ja mam wykładać kinetykę bez rachunku różniczkowego? Minima programowe robią wrażenie kpiny wyssanej z ministerialnego palca... Są jednak oznaki, że podejście do uczenia matematyki w szkołach, ulegnie szybkiej i pozytywnej zmianie.

Na jednej z Netowych grup dyskusyjnych padło pytanie o zadanie w którym pH zmienia się o (bodaj) dwie jednostki. Przytaczam znamienne fragmenty wymiany listów.

-proszę o wyrozumiałość... to właściwie mój pierwszy kontakt z logarytmami [z obliczaniem pH też]

-Gratulacje!
Tylko po co tyle pisać? Pamiętaj tylko, że zmiana pH o 1, to dziesięciokrotny spadek stężenia jednych jonów, i 10-krotny wzrost stężenia drugich jonów [tzn. H+ i OH-]

-tego nie wiedziałem...
w takim wypadku zadanie było banalne:)

-no bo widzisz, drogi kolego,  to nie było tak naprawdę zadanie z chemii, tylko  z podstaw matematyki. To, że zmiana pH o jednostkę oznacza 10-krotny wzrost  lub spadek stężenia jonów nie jest żadnym prawem chemicznym, tylko wynika z prostych właściwości logarytmów.
A swoją drogą... W jakiej to szkole nie uczą logarytmów ZANIM wprowadzą pojęcie pH?

-choćby w mojej - to była paranoja, gdy babka w 1 klasie mówiła o pH, a wszyscy na nią patrzyli jak na idiotkę... Do 3 klasy wszyscy liczyliśmy logarytmy tylko na kalkulatorze, nikt nie miał pojęcia po co ktoś sobie życie tak utrudnił by to dziadostwo wprowadzić... No aż wreszcie szanowna matematyczka wyłożyła nam funkcję logarytmiczną i już ją polubiliśmy (przynajmniej ja), bo została zrozumiana. I ot, koniec krótkiej historii wziętej ze szkolnego życia ucznia szkoły średniej.

 

A może zdarzył się cud - i ktoś z PT Czytelników polubił choć trochę logarytmy? Na ćwiczeniach laboratoryjnych z chemii analitycznej przeliczałem błędy wyników używając suwaka (to taka moja zemsta za studencki fetyszyzm kalkulatorowy). Jedna z dociekliwych Studentek (są takie jeszcze!) zapytała; co to takiego - taka linijka? Kiedy pokazałem, jak zamiast żmudnie mnożyć lub dzielić liczby, wystarczy dodawać lub odejmować odcinki w skali logarytmicznej, wykrzyknęła: KAPITALNE! Może więc warto, aby czasem ktoś spoza profesji pisał o rzeczach, na których się właściwie nic a nic nie zna... Czeka mnie jeszcze F opis idei rachunku różniczkowego (mocno się obawiam, że tolerancja matematyków zostanie jednak wyczerpana). Będę jednak to robił dopóty, dopóki wstępu do trygonometrii, logarytmów, rachunku różniczkowego itd. nie poprzedzi się krótkim wytłumaczeniem DLACZEGO warto zajmować się danym tematem - będącym po prostu wygodnym narzędziem do rozwiązywania bardzo praktycznych problemów. Nauczyciele: wstydźcie się...

 

LITERATURA
http://www.wiw.pl/nowinki/astronomia/200112/logarytmy.asp
http://www.wiw.pl/nowinki/matematyka/200102/20010205-001.asp
http://www.fizyka.umk.pl/~duch/books-fsk/historia/historia.html
http://solar.physics.montana.edu/kankel/math/csr.html
http://www.svpal.org/~dickel/OK/OKtypes.html
http://www.fourmilab.ch/bombcalc/brico.html
Świat Nauki Nr.6 (178) str. 74.   2006r
Wiedza i Życie wrzesień, str. 20 2002,  Komputer w linijce