REAKCJE OSCYLACYJNE:  MODELE FIZYCZNE SAMOORGANIZACJI CHEMICZNEJ

**ostatnia aktualizacja 13.05.2008**

chemiczne niezwykłości

Jeśli kiedykolwiek obserwowaliście reakcję oscylacyjną Biełousowa lub Briggsa-Rauschera, lub wędrujące fale reaktywności chemicznej, zapewne pozostawiło to niezapomniane wrażenie najbardziej niezwykłych procesów chemicznych.

Reakcja F Briggsa-Rauschera polega na zmieszaniu bezbarwnych roztworów jodanu zakwaszonego kwasem siarkowym, soli manganu, kwasu malonowego, nadtlenku wodoru i skrobi. Po kilkunastu sekundach mieszanina na moment barwi się złoto, a następnie granatowo. Po kilkunastu dalszych sekundach roztwór ponownie staje się bezbarwny, złoty, granatowy itd. Chemicy przyzwyczajeni są do monotoniczności zmian stężeń wszystkich reagentów. Tu jednak stężenia (przynajmniej niektórych reagentów) okresowo rosną, aby po chwili zmniejszać się do zera i tak dalej. Jak wahadło zegara... (potem okaże się, że jednak niezupełnie tak samo)

http://www.youtube.com/watch?v=Ch93AKJm9os&feature=fvwrel         http://www.youtube.com/watch?v=ehIzNln90-I&feature=related (tu reakcja Biełousowa-Żabotyńskiego, a nie Briggsa-Rauschera)

Z reguły pada wtedy pytanie: jaki jest mechanizm podobnej reakcji? Jak to możliwe, aby reakcja chemiczna mogła zachowywać się w taki niezwykły, zorganizowany sposób?

Mechanizm “modelowej” reakcji Biełousowa jest dziś już znany i obejmuje ok. 23 sprzężonych reakcji. Odmawiam jednak najczęściej napisania tego ciągu równań. Bo i tak na zakończenie padnie pytanie: “ale dlaczego ten ciąg reakcji nie prowadzi monotonicznie do stanu równowagi, ale pojawiają się oscylacje?” Przyczyna tych dziwacznych zachowań jest natury termodynamicznej, a nie chemicznej. Dlatego poniżej formułuję owe warunki termodynamiczne i podaję ich modelową ilustrację. Wreszcie wskazuję, w jaki sposób spełnione zostają te wymogi termodynamiczne - na sposób chemiczny. Zaawansowani matematycznie specjaliści od nieklasycznej termodynamiki będą na pewno bardzo zgorszeni uproszczeniami tego opisu. Chciałbym jednak odwołać się do analogii i sprawić, że czytelnicy będą emocjonalnie skłonni dopuścić możliwość takiego przebiegu reakcji chemicznych w pewnych przypadkach. Bo matematyczny opis teorii katastrof jest zbyt abstrakcyjny również i  dla piszącego ten długi wywód... Proszę przygotować się do wprowadzenia kilku pojęć, które w pierwszej chwili mogą brzmieć egzotycznie; będą jednak podane ich fizyczne interpretacje.

Bardzo charakterystyczne jest zachowanie tych chemików “starej daty”, którzy widzą tę reakcję po raz pierwszy. Czasem w milczeniu oglądają podejrzliwie naczynie ze wszystkich stron, szukając oszustwa na które próbuje się ich nabrać. A czasem wręcz oświadczają, że “to jest niemożliwe!”. Podobnie jak w znanej anegdocie o dwóch poczciwcach w ZOO, którzy zobaczyli po raz pierwszy żyrafę (“ty nie wierz własnym oczom: takie zwierzę nie istnieje”). Stąd zapewne pochodzi popularne określenie podobnych procesów: “termodynamiczne ZOO”. Przez wiele lat środowisko naukowe odrzucało jakąkolwiek interpretację zjawisk samoorganizacji, powołując się na drugą zasadę termodynamiki. Środowisko naukowe uchodzi za bardzo otwarte na nowe idee, jednak granicą tej otwartości jest właśnie uznanie zachowania zasad termodynamiki. Nazwano to nawet “termodynamicznym paradygmatem”. Tymczasem zasady termodynamiki w tych procesach nie są pogwałcone! Trzeba tylko rozumieć je szerzej. A Zasady termodynamiki tak dalece nie mają głębszego uzasadnienia teoretycznego, że do dziś nie dostąpiły rangi zakwalifikowania ich jako Prawa fizyczne...

WARUNEK PIERWSZY: głębokie niezrównoważenie...

Lokalnie mogą przebiegać samorzutne procesy o malejącej entropii, np. procesy samoorganizacji czasowej lub przestrzennej. Napędzane one są przez towarzyszący im wzmożony wzrost entropii w innych obszarach. W układzie wraz z otoczeniem, entropia sumarycznie więc rośnie. W ten sposób właściwie sformułowałem już pierwszy warunek konieczny do powstania samoorganizacji. Miarą samorzutności jest wartość F energii swobodnej procesu. Reakcje samoorganizacji wymagają szczególnie silnie ujemnej energii swobodnej. Ponieważ energia swobodna jest czasem interpretowana jako miara odchylenia od równowagi, można sformułować to, jako warunek dostatecznie dużego odchylenia od równowagi. Ponieważ procesy te są tak samo niezwykłe, jak opisy science-fiction, czasem używane jest określenie wręcz psychiatryczne: “procesy głęboko niezrównoważone”. Nie jest to aż tak bardzo zabawne, bo F B.Biełousow - odkrywca najsłynniejszej z tych reakcji i jego próby publikacji tego odkrycia - były tak brutalnie odrzucane przez środowisko naukowe, że musiał szukać specjalistycznej pomocy lekarskiej...

Borys .Biełousow

Warunek silnie ujemnej energii swobodnej jest wbrew pozorom zdefiniowany bardzo precyzyjnie. Oznacza on, że odchylenie od równowagi musi być większe od  pewnej ściśle sprecyzowanej wartości progowej.

model butelki i progowe odchylenie od równowagi

Modelem układu fizycznego w stanie równowagi niech będzie stojąca butelka z wodą. Siły działające na układ są zrównoważone (ciężar wody i sprężystość podłoża) i układ znajduje się w stanie stabilnej równowagi. Jeżeli butelkę przechylić (układ zostaje odchylony od stanu równowagi) o kąt tak duży, aby poziom wody znalazł się powyżej dolnej krawędzi otworu szyjki, powstaje niezrównoważona siła, która spowoduje wypływ wody. Wypływ będzie miał przebieg monotoniczny, aż do ustalenia nowego stanu równowagi. Jeśli butelkę przechylić silniej (o większy kąt), to wypływ staje się bardziej raptowny; ciągle ma on jednak monotoniczny charakter. Dla każdej butelki z wodą istnieje bardzo dokładnie określony kąt, po przekroczeniu którego zupełnie zmienia się jakościowy charakter wypływu. Wypływ zaczyna być pulsacyjny!

W typowych chemicznych reakcjach oscylacyjnych i innych zjawiskach samoorganizacji, siłą napędową jest potencjał chemiczny, czyli mówiąc najprościej, użycie silnie reaktywnych substratów (np. energicznych reduktorów i energicznych utleniaczy) użytych w dostatecznie wysokim stężeniu. Ponieważ w miarę upływu czasu stężenia substratów maleją na skutek ich przereagowania, maleje również napędowy potencjał chemiczny procesu. Z chwilą gdy obniży się on do pewnej granicy progowej, zanika oscylacyjny charakter zmian, a dalsza reakcja ma już klasyczny, monotoniczny przebieg.

Stan równowagi jest synonimem martwoty i stagnacji, natomiast odchylenie od równowagi jest stanem, który niesie możliwość dziania się i innowacji. Właściwie wszystko, co dziś jeszcze gdziekolwiek się dzieje - jest odległym szczątkowym echem gigantycznego niezrównoważenia i fluktuacji w odległym momencie “zerowym” - jakkolwiek by go nazwać.

stany ustalone stabilne i niestabilne

Jesteśmy przyzwyczajeni, że z reguły układy mają jeden stabilny stan równowagi. Wyobraźmy sobie jednak ołówek z zaostrzonym końcem postawiony pionowo. Jeśli ustawiony jest on dokładnie na ostrzu, to nie działają żadne niezrównoważone siły; taki stan nazywany jest stanem ustalonym lub stacjonarnym. Stany ustalone mogą być zarówno stabilne, jak i niestabilne. Do doświadczalnego zbadania jego stabilności można posłużyć się metodą zaburzeń. Jeśli taki postawiony na ostrzu ołówek bardzo nieznacznie odchylić, pojawi się niezrównoważona siła boczna, która po chwili zwiększy owo odchylenie, co doprowadzi do jeszcze większego niezrównoważenia i odchylenia... Jest to typowy obraz niestabilnego stanu ustalonego. Można wyobrazić sobie jeszcze jeden stan ustalony: zwisającego ołówka przywiązanego nitką (lub zaostrzonego gwoździa i płaskiej sztaby magnetycznej). W stanie tym ołówek zwisa swobodnie na nitce jak wahadło. Tu również nie działają żadne siły niezrównoważone. Jednak próba odchylenia z tego stanu powoduje powstanie siły, która zmniejsza pierwotne zaburzenie i przesuwa układ w kierunku stanu początkowego. Jest to więc stabilny stan ustalony. Typowym takim stanem jest stan równowagi. Podziałanie jakiegokolwiek zaburzenia, z reguły skierowuje układ w stronę jakiegoś stanu równowagi; mówi się, że stan równowagi jest więc najsilniejszym atraktorem. Tak więc niektóre układy mogą mieć kilka stanów ustalonych: niestabilnych i stabilnych.

wielokrotne niestabilne stany ustalone: oscylator solankowy

Zachęcam do zbudowania doskonałego modelu-zabawki: hydraulicznego oscylatora solankowego Martina. Przygotować korpus szklanej strzykawki; w wylocie za pomocą kropli roztopionej parafiny wkleić szklaną kapilarę o wewnętrznej średnicy ok. 0,5 mm. Strzykawkę napełnić stężonym roztworem cukru (działa lepiej niż proponowany oryginalnie roztwór soli), z niewielkim dodatkiem NaOH. Strzykawkę wstawić do dużego pojemnika z odgazowaną wodą z dodatkiem fenoloftaleiny (np. cylinder miarowy z przegotowaną i ostudzoną wodą), i umocować np. za pomocą klamerek. Fenoloftaleina i NaOH nie są niezbędne; ułatwiają jedynie obserwacje funkcjonowania modelu. Przy jednakowych poziomach wody zewnątrz oraz roztworu w strzykawce, roztwór zaczyna wypływać w dół - z powodu niezrównoważenia spowodowanego większym ciężarem właściwym roztworu. Z chwilą obniżenia się poziomu wewnątrz strzykawki i zrównania parcia zewnętrznego i wewnętrznego, układ osiąga stan ustalony i wypływ ustaje. W tym stanie istnieje równowaga parć:

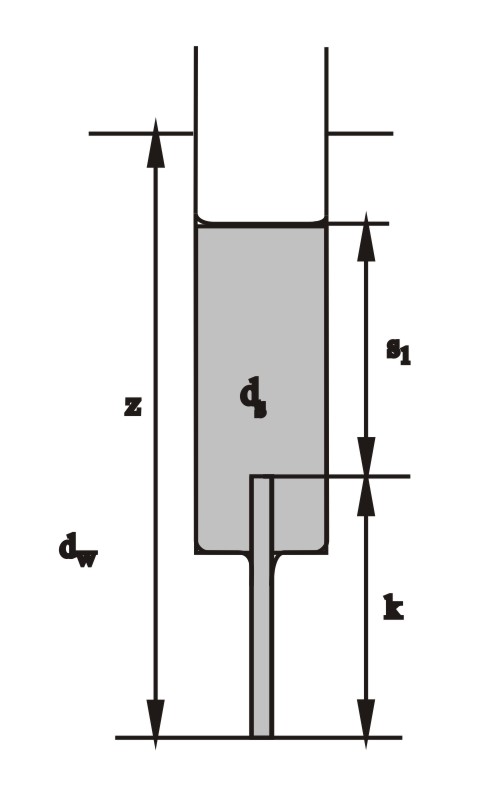
d_wz = d_ss₁ + d_sk

Można się od razu domyślić, że jest to stan niestabilny, bo przecież jest to sytuacja, gdzie roztwór o większym ciężarze właściwym usytuowany jest wyżej, niż lżejsza czysta woda. Po kilku sekundach, na skutek zadziałania jakiejś przypadkowej fluktuacji, rozpoczyna się wpływ wody z zewnątrz do kapilary i do wnętrza strzykawki. Dostanie się choćby najmniejszej ilości wody do kapilary powoduje zanik zrównoważenia parć i powoduje niezrównoważenie, i jeszcze gwałtowniejsze wpływanie wody do kapilary. Proces ten przebiega coraz gwałtowniej, bo towarzyszy mu wzrost niezrównoważenia, a opory przepływu maleją: lepki roztwór cukru w kapilarze jest zastępowany czystą wodą. Jest to nieliniowy proces odpowiadający autokatalizie w reakcji chemicznej. Po pewnym czasie ustala się wyższy poziom roztworu (teraz już nieco rozcieńczonego), w którym następuje znowu zrównanie parć (tym razem kapilara napełniona jest czystą wodą).

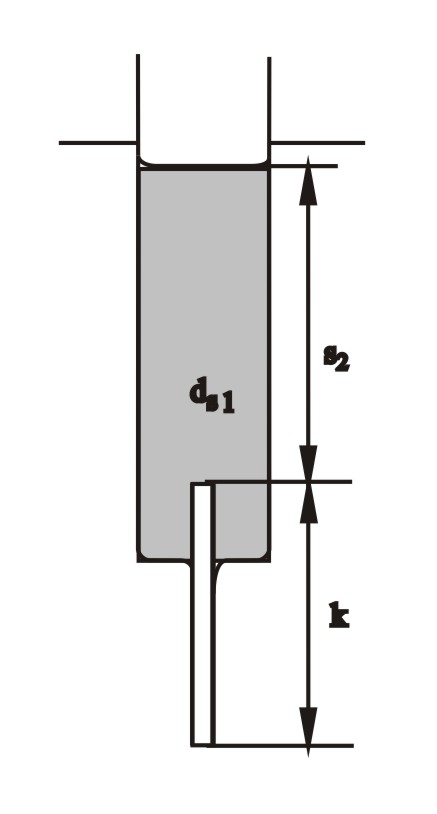
d_wz = d_s1s₂ + d_wk

Ten drugi stan ustalony jest również stanem niestabilnym (ciągle przecież cięższy roztwór jest położony wyżej niż czysta woda). Przypadkowe zakłócenie spowoduje lawinowo przyspieszający wypływ roztworu w dół. Oscylacje mogą trwać wiele godzin.

Niżej: dwa zdjęcia-zbliżenia: początku fazy wpływania wody przez kapilarę do strzykawki, oraz początku fazy wypływania roztworu cukru z kapilary w dół; kształty słupków cieczy są bardzo charakterystyczne, z zaznaczonym grzybkowatym frontem fali uderzeniowej.

Podsumujmy: układ jest początkowo silnie odchylony od stanu równowagi (duże stężenie, duży ciężar właściwy roztworu). Ma on dwa niestabilne stany ustalone, kinetyka ma nieliniowy charakter. Układ dąży do równowagi poprzez kolejne oscylacje pomiędzy dwoma tymi niestabilnymi stanami ustalonymi. Strumienie cieczy można doskonale obserwować i filmować nawet bez dodatku fenoloftaleiny, wykorzystując różnice współczynników załamania światła (tak jak w mikroskopie fazowo-kontrastowym).

oscylator elektryczny z neonówką

Proponuję zbudowanie prostego układu elektrycznego, którego opis jest uderzająco podobny do logistycznego opisu funkcjonowania chemicznej reakcji oscylacyjnej.

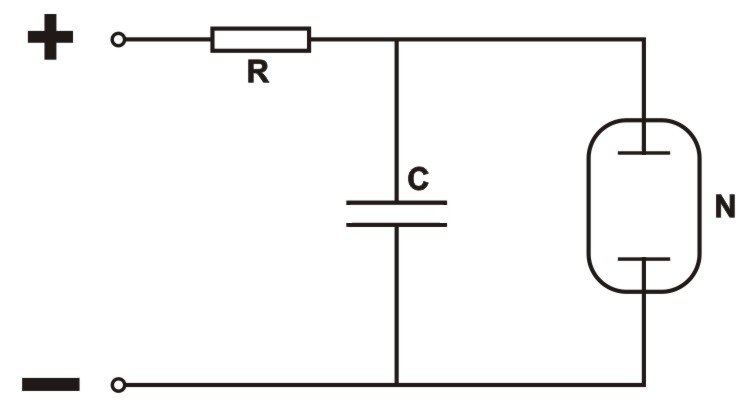
Kondensator C jest ładowany stałym napięciem (ew. napięcie zmienne + dioda) poprzez opornik R. Do kondensatora równolegle podłączona jest neonówka N. Napięcie na okładkach kondensatora rośnie w czasie według zależności zbliżonej do logarytmicznej. Z chwilą osiągnięcia progowej wartości napięcia następuje zapłon neonówki. Zapłon jest procesem nieliniowym: zjonizowane pojedyncze elektrony zostają tak silnie przyspieszone w polu elektrycznym, że lawinowo jonizują wiele innych atomów gazu. Ale zapalona neonówka doskonale przewodzi prąd i powoduje gwałtowne obniżenie napięcia na kondensatorze. Z chwilą gdy napięcie spadnie poniżej wartości która podtrzymuje stan zjonizowania gazu w neonówce, następuje lawinowy proces rekombinacji plazmy i gaz przestaje przewodzić: neonówka gaśnie. Teraz zaczyna się proces ponownego ładowania kondensatora aż do powtórnego rozbłysku.

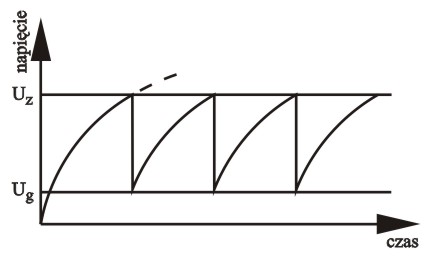
Podsumujmy: układ jest w stanie silnego niezrównoważenia (napięcie zasilające musi być chociaż trochę wyższe od wartości napięcia zapłonu neonówki). Układ ma dwa niestabilne stany ustalone. Kinetyka ma nieliniowy charakter. Podanie stałego napięcia na wejściu w tych warunkach powoduje powstanie oscylacji. Kształt krzywej jest bardzo zbliżony do zmian stężeń podczas chemicznych reakcji oscylacyjnych.

intymne życie funkcji matematycznych: nieliniowość, katastrofy, punkty czułe...

Zadaję czasem pytanie: która funkcja rośnie szybciej: kwadratowa (nieliniowa)   y = x², czy liniowa   y = x ? Z reguły wszyscy wskazują na funkcję kwadratową... A przecież wszystko zależy od przedziału zmienności: dla wartości zmiennej x od zera do jedności, szybciej rośnie (mam na myśli wartości funkcji, a nie wartość pochodnej) funkcja liniowa (!) , a dla wartości większych niż 1 - funkcja kwadratowa.

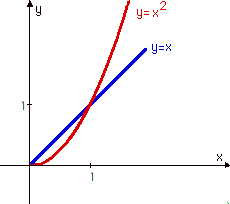
Punkt x=1 jest punktem szczególnej niestabilności: nawet nieskończenie mała zmiana parametru x prowadzi do zupełnie zasadniczych różnic zachowania się takiego układu funkcji. W punkcie x=1 następuje katastrofa. Podobnie jak podczas naciskania ściennego przełącznika oświetlenia. Stopniowe uginanie przełącznika nie powoduje zmiany stanu stabilności. Dopiero osiągnięcie pewnego jego położenia wprowadza w stan niestabilności. Utrzymanie takiego stanu jest praktycznie niemożliwe: po oderwaniu palca zawsze następuje albo przełączenie, albo powrót do stanu pierwotnego (sami zresztą spróbujcie!).

Oszałamiającym obrazem graficznym owego "życia" funkcji matematycznych są Fraktale (sięgnij do odsyłaczy na końcu).

Wyobraźmy sobie dwie reakcje przebiegające według różnego typu kinetyki/rzędowości:

            A + B = C + D   według kinetyki np. pierwszego rzędu   v = k x [A]

oraz odwrotną reakcję

            C + D = A + B   według  kinetyki np. drugiego rzędu   v = k x [C] ²

(przypominam, że rząd reakcji może nie mieć nic wspólnego ze współczynnikami i postacią równania sumarycznego).

Chemicy zapisują to w skrócie jako:

            A + B <=> C + D

i jest dla nich oczywiste, że układ taki szybciej lub wolniej prowadzi do stanu równowagi dynamicznej. Tylko, że termodynamika nie opisuje sposobu dochodzenia do stanu końcowego, a tu właśnie zajmujemy się opisem warunków, w których jest to droga niezwykła: jako szereg następujących po sobie oscylacji...

To, w jakim kierunku nastąpi postęp reakcji mieszaniny tych czterech substancji, zależy od tego, która kinetyka jest szybsza: przemiana w prawo, w kierunku powstawania C + D (opisywane przez zależność liniową), czy w lewo, w kierunku A + B (opisywane przez zależność nieliniową). A to zależy od tego, czy stan początkowy leży w zakresie punktu niestabilności (katastrofy), czy też w zakresie jednego z dwóch obszarów stabilności. A jeśli w jakimś złożonym procesie istnieją dodatkowe mechanizmy kierujące układ w stronę punktu niestabilności (lub istnieją mnogie punkty niestabilne) - to możliwe staje się wielokrotne przełączanie kierunku biegu reakcji. Musi istnieć dodatkowe sprzężenie zwrotne tych mechanizmów.

nieliniowość na sposób chemiczny: powielanie w autokatalizie

Możliwe jest otrzymanie oscylujących modeli nawet na układach liniowych. Tu można uruchomić taki F program komputerowy, autorstwa Pana Zygmunta Trumpakaja (dzięki za udostępnienie!).

Również: http://www.youtube.com/watch?v=A2mnpSY3gBg

Z reguły oscylujące układy chemiczne oparte są jednak na jakimś mechanizmie nieliniowym (kinetyka rzędu wyższego niż pierwszy), a prócz tego, na procesach autokatalizy lub autoinhibicji. Przypominam, że doskonałym modelem takiego prostego mechanizmu autopowielania-autokatalizy jest F reakcja Landolta. W reakcji Landolta kluczowy jest proces powielania, który zapisać można jako:

        I^–  →  [ ... ]  → 1,2 I^–

Odsyłam do opisu reakcji Landolta, aby uniknąć wątpliwości, że zapis taki jest sprzeczny z zasadą zachowania masy. Podobnie rozumieć należy zapis:

        K → 2 K,   który pojawi się później przy opisie modelu Lotki-Volterry

oscylator Lotki-Volterry, Oregonator, Brukselator, Bubbelator, oscylator ekologiczny

Już w roku 1910 A.Lotka zaproponował model matematyczny oscylatora; tu zamieszczam opis jego modyfikacji znanej jako model Lotki-Volterry. Dane są trzy sprzężone procesy opisywane przez równania:

T + K → 2 K

K + L → 2 L

L → P

Dla określonych parametrów równań kinetycznych oraz dla pewnych wartości początkowych można wykazać (program komputerowy), że liczebności populacji pośrednich K i L nie dążą do stabilnych wartości równowagowych, ale zmieniają się w sposób oscylacyjny! Zaproponowano jeszcze wiele innych modeli oscylatorów.

Słuszność modelu znalazła potwierdzenie w badaniach ekologicznych na północy Kanady. W uproszczeniu proszę sobie wyobrazić środowisko dostarczające nieograniczonego zapasu trawy (T), na którym żyje populacja królików (K), w tak sprzyjających warunkach rozmnażających się lawinowo (T + K → 2 K). Jeśli w tym środowisku żyje także populacja lisów odżywiającymi się królikami, to po pewnym czasie następuje lawinowy wzrost populacji lisów (K + L → 2 L). Po pewnym czasie powoduje to czasowy spadek populacji królików, a w konsekwencji, po kolejnym przesunięciu w czasie - także populacji lisów. Spadek populacji drapieżników po pewnym czasie skutkuje odrodzeniem się populacji królików... Ostatni proces, to następująca stale śmiertelność lisów.     http://www.youtube.com/watch?v=A2mnpSY3gBg 

Doskonale znana jest gradacja świerszczy występująca na Wyspach Brytyjskich z zadziwiającą dokładnością: dokładnie co 15 lat! Typowym oscylacyjnym procesem ekologicznym jest masowa gradacja owadzich szkodników lasów występująca mniej regularnie co kilkadziesiąt lat. Nie są to więc przypadkowe zjawiska, ale złożone procesy oscylacyjne.

wreszcie: mechanizm Reakcji Biełousowa

Jeśli teraz już emocjonalnie przyjmujecie, że układy fizyczne lub ekologiczne mogą funkcjonować w trybie oscylacyjnym, to jest już czas na opis chemicznej reakcji oscylacyjnej... Po zmieszaniu zakwaszonego roztworu bromianu, kwasu malonowego, soli ceru oraz wskaźnika - ferroiny, przez pewien czas istnieje stan indukcji. Szczegółowy mechanizm Reakcji jest bardzo zawiły i nie będzie tu podany. Obejmuje trzy grupy złożonych procesów, które będą jedynie pokrótce opisane. Proszę zwrócić uwagę, że w tym opisie występują wszystkie przytaczane wcześniej elementy termodynamiczne.

W roztworze początkowo istnieje pewne stężenie jonów bromkowych, które pełnią kluczową rolę w całym mechanizmie. Jony bromkowe są powoli usuwane w wyniku utleniania bromianem:

2Br^– + BrO₃^–  + 3CH₂(COOH)₂ + 3H⁺  = 3CHBr(COOH)₂ + 3H₂O      A

W wyniku reakcji A stężenie jonów bromkowych stopniowo maleje. Z chwilą, gdy spadnie ono poniżej pewnej dolnej wartości progowej, zachodzi raptowne utlenienie jonów cerawych do jonów cerowych:

 4Ce³⁺ + BrO₃^–  + CH₂(COOH)₂ + 5H⁺  = 4Ce⁴⁺ + CHBr(COOH)₂ + 3H₂O     B

Jest to reakcja autokatalityczna, która jest skutecznie hamowana przez jony bromkowe. Aby mogła zajść, trzeba poczekać, aż stężenie jonów bromkowych spadnie poniżej pewnej dolnej wartości progowej. W wyniku autokatalizy jony ceru bardzo raptownie przechodzą w postać utlenioną; towarzyszy temu gwałtowna zmiana barwy wskaźnika na niebieski.

W kolejnej fazie powstały kwas bromomalonowy zostaje utleniany, uwalniane są aniony bromkowe, których stężenie rośnie w wyniku reakcji C szybciej, niż ich konsumpcja w reakcji A. Stężenie utlenionej postaci ceru maleje, a wskaźnik stopniowo zmienia barwę na różową.

4Ce⁴⁺ + CHBr(COOH)₂ + 2H₂O = Br^– + 4Ce³⁺ +  HCOOH + 2CO₂ + 5H⁺     C

Po przekroczeniu pewnej górnej wartości progowej stężenia bromku, następuje ponowne zablokowanie autokatalitycznej reakcji B (autoinhibicja). Powstają duże ilości jonów bromkowych. Trzeba odczekać, aż zostaną one skonsumowane w reakcji A. Potem cykl zostaje kolejny raz odtworzony. Oscylacje zachodzą tylko do czasu osiągnięcia minimalnego granicznego odchylenia od stanu równowagi; dalszy przebieg ma charakter monotoniczny.

Podsumowuję charakterystyczne elementy logistyczne układu oscylującego: znaczne odchylenie od stanu równowagi osiąga się przez użycie odpowiednio stężonych, energicznych utleniacza i reduktora. Jest to układ sprzężonych ze sobą reakcji o przebiegu nieliniowym: autokataliza i inhibicja. Istnieją dwa stany ustalone, którym odpowiada istnienie katalizatora (Ce) w dwóch stanach: utlenienia (Ce⁴⁺) i redukcji (Ce³⁺). Oraz systemu sprzężonych reakcji stabilizujących i destabilizujących, pozwalających na przechodzenie pomiędzy tymi skrajnymi stanami. Jony bromkowe z dwoma poziomami progowymi ich stężeń pełnią rolę przełącznika blokującego i odblokowującego ciągi reakcyjne. Oscylacjom podlega stężenie jonów bromkowych oraz stosunek stężeń obu form katalizatora-ceru (można te zmiany śledzić za pomocą wskaźnika redoks - ferroiny).

Reakcja Briggsa-Rauschera jest jeszcze atrakcyjniejsza, bo oscylacje są bardzo kontrastowe (bezbarwny-złoty-granatowy) i bardzo szybkie: co kilkanaście sekund; a jej uruchomienie jest bardzo proste. Reagenty: zakwaszony roztwór jodanu, kwasu malonowego, nadtlenku wodoru, katalizowany solą manganawą, z dodatkiem skrobi. Mechanizm tej reakcji jest słabo poznany; prawdopodobnie są to dwie sprzężone reakcje oscylacyjne. Do konkretnych przepisów odsyłam do literatury na końcu opracowania.

**sprzężone oscylatory

Wspomniano o złożonym charakterze reakcji Briggsa-Rauschera. Bardzo charakterystyczna jest skłonność układów oscylujących do samosynchronizacji. Zegarmistrze znają fakt wzajemnego oddziaływania chodu dwóch zegarków położonych obok siebie na twardym podłożu. Tu proponuję obejrzenie filmów z synchronizacji metronomów:

http://www.youtube.com/watch?v=tlYIyKic3w8&feature=related synchronizacja 3 metronomów

http://www.youtube.com/watch?v=W1TMZASCR-I&feature=related 5 metronomów

http://www.youtube.com/watch?v=kqFc4wriBvE 34 metronomy

http://www.youtube.com/watch?v=2JzMJNMYbRw&feature=related chaotyczne wahadło

http://www.youtube.com/watch?v=wQ-MC71ffB8&feature=related chaotyczny oscylator

http://www.youtube.com/watch?v=DxQ1BjQcicg&feature=related chaos spiralny **

termodynamiczne ZOO

Wspomniałem poprzednio o samoorganizacji chemicznej w postaci oscylacji czasowych. Prócz tego znanych jest bardzo wiele innych podobnych zjawisk. Jednym z najniezwyklejszych, jest samoorganizacja przestrzenna w postaci F kolorowych wędrujących fal reaktywności chemicznej.

A również tak abstrakcyjne, jak bi- (i wielo-) stabilność, deterministyczny chaos (powstawanie zorganizowanych struktur w nieprzewidywalny jednak, chaotyczny sposób). Równie fascynujące, a niemal nieznane są fizyczne zjawiska w rodzaju wirów, ścieżek Kármana lub konwekcji Bénarda, strącania osadów w postaci F pierścieni Lieseganga.

http://www.youtube.com/watch?v=Bn2u__1Q0TQ&feature=related

http://www.youtube.com/watch?v=UhImCA5DsQ0&feature=related

http://www.youtube.com/watch?v=nfvHIfzVnt0&feature=related

http://www.youtube.com/watch?v=WMOyddQxDBE&feature=related

Zupełnie niezwykły film dotyczy innego jeszcze zjawiska:

http://www.youtube.com/watch?v=A5OhZ9wT568&feature=related

pogwałcona termodynamika?

Dlaczego w procesach fizycznych zjawiska oscylacji są często spotykane, jak np. w przypadku wahadła lub sprężyny, natomiast w reakcjach chemicznych są one aż tak wielką rzadkością? Obiekty fizyczne złożone z miliardów atomów stanowią często jednak zwarty obiekt, który zachowuje się jak jedna całość. W reakcjach chemicznych jest to najczęściej roztwór zawierający również miliardy cząsteczek, które jednak są od siebie w znacznym stopniu niezależne. I do ich opisu stosują się zasady statystyki. Prawo wielkich liczb powoduje uśrednienie losów pojedynczych cząsteczek i opis makroskopowych zmian zawartości zlewki jako całości - jest najczęściej monotoniczny.

W procesach samoorganizacji druga zasada termodynamiki jest zachowana. W miarę upływu czasu coraz mniejsze są stężenia substratów, a rosną stężenia produktów. Zupełnie nietypowy staje się jednak opis losów pojedynczych elementów zbiorowiska w stanie oscylacji. Gdyby dało się prześledzić losy pojedynczej wybranej cząsteczki w trakcie klasycznej reakcji chemicznej (np. obserwując ją przez jakiś niezwykły mikroskop), okazałoby się, że losy jej są w zasadzie nieprzewidywalne. Można tylko statystycznie przypuszczać, że w początkowej fazie reakcji obserwowana cząsteczka będzie raczej cząsteczką substratu, natomiast w miarę upływu czasu, coraz bardziej prawdopodobnie będzie już to cząsteczka produktu. W tym sensie zwykła reakcja chemiczna jest przykładem nieuporządkowania (przypadkowości, bezładu).

Zupełnie odmienna jest sytuacja podczas reakcji oscylacyjnej, np. reakcji Briggsa-Rauschera. Wszystkie cząsteczki związków jodu w pewnym momencie znajdują się w formie utlenionej (I₂, niebieski). Z całą pewnością można przepowiedzieć, że w np. 15 sekund później wszystkie te cząsteczki będą (jak na gwizdnięcie!) znajdować się w formie zredukowanej (I^–, bezbarwny). I tak dalej. A więc determinizm zamiast przypadkowości!

narastające fluktuacje i szkoły policyjne

Inna osobliwość dotyczy powstawania i dalszego losu fluktuacji (czyli przypadkowego powstania odchyleń od stanu najbardziej prawdopodobnego) w układach silnie niezrównoważonych. W stanie bliskim równowagi fluktuacja jest tym mniej prawdopodobna im jest ona większa. Istniejące już fluktuacje po pewnym czasie zostają uśrednione. Im fluktuacja jest większa, tym rzadziej ona powstaje i tym gwałtowniej ona zanika. Można by to wręcz sformułować jako jeszcze jedną zasadę termodynamiki.

Zupełnie inna jest sytuacja w układzie silnie odchylonym od równowagi. Dostatecznie duże fluktuacje nie tylko nie zanikają, ale mają tendencję do rozszerzania się na cały układ. Tak powstają np. wędrujące fale reaktywności chemicznej.

Niech analogią będzie zachowanie widowni na stadionie. Podczas mało emocjonującego meczu panuje atmosfera ospałości. Pojedynczy wybryk podpitego kibica np. “bij sędziego!” (nieznaczna fluktuacja) nie zostaje podjęty i szybko ginie w sennym otoczeniu. Zupełnie inna sytuacja jest podczas napiętej atmosfery ostatnich sekund spotkania o wielką stawkę. Taki sam wybryk kibica zostaje podjęty przez otoczenie i ma tendencję do rozszerzenia na cały układ, przyjmując znane i godne ubolewania zwierzęce formy niszczącego amoku widowisk sportowych (tak, przyznaję: nie znoszę sportu!). Nie ma się co dziwić, że pewne elementy teorii katastrof są wykładane w szkołach policyjnych.

Ale analogię można odwrócić i potraktować roztwór w fazie indukcji wykluwania się oscylacji lub fal aktywności - jako “spięte” zbiorowisko “oczekujące” tylko na jakąś fluktuację.

o roli drylu wojskowego; porozumiewające się cząsteczki

Analogie do drylu wojskowego są uderzające. Najpierw stwarza się stan, w którym poszczególne osoby (żołnierze) zatracają poczucie swojej indywidualności i stają się jedynie częścią oddziału (“stanem osobowym”). Dokonuje się tego długą musztrą, która wydaje się równie bezsensowna, jak jednolitość stroju (np. przymus noszenia znienawidzonej przeze mnie czapki, nawet w upał) - a która ma na celu właśnie owo zniszczenie podświadomej indywidualności i zastąpienie ich działaniami zbiorowymi (polecam lekturę “Na zachodzie bez zmian” E.Remarque’a). I wytwarzania stanu bezustannego napięcia poprzez psychiczne maltretowanie. Następnie mitologizuje się mistyczność “rozkazu wojskowego” (owe: “baczność” , "pal", "służba wartownicza").

Stan indukcji reagentów tuż przed powstaniem oscylacji ma podobne cechy: istnieje gotowość do zbiorowego reagowania na impuls pobudzający. Ale ów impuls trzeba również odebrać i wykonać działanie spójne z innymi cząsteczkami. Wprowadzono termin: oddziaływanie informacyjne o zasięgu makroskopowym pomiędzy cząsteczkami. Takie potraktowanie wydaje się raczej właściwe dla powieści S.F., wprowadził je jednak Ilia Prigogine, laureat Nagrody Nobla. Trudno oczywiście dziś opisać, na czym miałoby polegać owo przekazywanie informacji pomiędzy cząsteczkami.

Atmosfera ciągłej presji i stresu (pozornie bezsensowne maltretowanie fizyczne i psychiczne, „fala”) charakterystyczna dla wojska, nie jest przypadkowa: jest ona czynnikiem podobnym jak silne odchylenie od stanu równowagi podczas reakcji chemicznej. Dopiero w takim stanie zbiorowiska wykazują szczególną skłonność do spójnych zachowań grupowych. A to jest cecha szczególnie pożądana przez dowództwo. Oficjalne tego zaprzeczanie ma charakter tylko propagandowy: kto ma ochotę, niech w to uwierzy. W wojsku zachowania spójne są wymuszone, i mogą przynosić skrajnie destrukcyjne skutki - gdy wojsko pozostaje bez należytej kontroli cywilnej.

Zawsze dziwię się ludziom, którzy w organizacji wojskowej dostrzegają nieodpartą atrakcyjność; we mnie budzi ona raczej obawy. Ale skłonność do spójnych działań zbiorowych tkwi głęboko w naszej podświadomości. Wspomnę tu o nieporównanej satysfakcji towarzyszącej dobrowolnemu uczestnictwu w wykonaniu muzyki chóralnej lub w zespole instrumentalnym. Nigdy nie zaznają tego wspaniałego uczucia młodzi ludzie owładnięci wizją solowego muzykowania (którzy jak złośliwie mawia A.Poniedzielski: “najpierw śpiewają, a potem dopiero komponują”. Zresztą dźwięki te mało mają wspólnego ze śpiewaniem; często chodzi o masturbację mózgu za pomocą lawiny łomotu i niemelodyjnego pojękiwania. Nieszczęśnicy ci nigdy nie poznają wyrafinowanego smaku  Koncertów Brandenburskich  J.S.Bacha - i pozostaną w kręgu fascynacji dźwiękiem godnym czkawki lub młota pneumatycznego...)

Zastanawiałem się kiedyś nad niezwykłością F Stanu Aromatycznego: sześcioczłonowy płaski pierścień i pływające nad i pod nim sprzężone i zdelokalizowane, przenikające się jak w menuecie - elektrony, które w tym tańcu zatraciły swój pojedynczo-podwójny stan wiązalności. Co jest powodem owej skłonności do powstawania związków aromatycznych, i ich trwałości? A może „odczuwają one szczególną przyjemność” z takiej harmonii, podobnie jak uczestnicy perfekcyjnie zgranego sekstetu wokalnego w prawosławnej cerkwi? Proszę wybaczyć odległe i nienaukowe skojarzenia, ale opisywane tu zachowania cząsteczek są bardzo niezwykłe, a jednocześnie czasami tak bardzo podobne do zachowania zbiorowisk ludzkich... 

Pewnie zdarzyło się Wam iść wraz z kimś, drogą. Jeśli tempo marszu stopniowo wzrastało, to po przekroczeniu pewnej progowej szybkości pewnie spostrzegliście, że podświadomie idziecie obok swego towarzysza wraz z nim, “w nogę”... Dlaczego? Przecież (o ile nie idzie się pod rękę) taki sposób marszu nie jest w niczym wygodniejszy? Tak objawia się nasza podświadoma skłonność do zachowań grupowych; mają ją również pojedyncze cząsteczki...

Jeden z odkrywców niezwykłego zjawiska wędrujących fal reaktywności chemicznej, T.Winfree, badał warunki, w których w audytorium sali koncertowej powstaje samoorganizacja w postaci aplauzu “standing owation” (i publikował w naukowym czasopiśmie prace na ten temat...). Zresztą sami pewnie znacie ową emocjonalną presję otoczenia sali, abyście w momencie takiego aplauzu wstali i klaskali nawet wtedy, gdy wcale nie macie na to akurat ochoty... Gorzej, gdy taka presja sprzyja powstawaniu społecznej dyktatury, jak np. w Niemczech w latach 30-tych (niełatwo zachować taki dystans, jak ów szczupły starszy pan w okularach i czapce, na tym filmie...).

polska wersja (włącz napisy-komentarze do filmu...) F https://www.youtube.com/watch?v=a5Qz4HvdmXw

Bo analogie z ekspandowaniem sfer politycznych i gospodarczych świata, są uderzające. Inny równie groźny, a zupełnie współczesny przykład: F "Defilada".

czy jesteśmy mieszanym reaktorem przepływowym?

To co opisano wyżej, dzieje się przy prowadzeniu reakcji oscylacyjnej w zlewce, czyli w układzie zamkniętym. Ewentualne oscylacje mają tu charakter gasnący. Do badania zjawisk samoorganizacji wygodniejsze jest prowadzenie reakcji w reaktorze zasilanym w sposób ciągły roztworami reagentów, i ciągłym odprowadzaniu nadmiaru roztworu - a więc w układzie otwartym. W tych warunkach nie tylko oscylacje mają charakter niegasnący, ale obserwować można inne niezwykłe formy samoorganizacji (dwustabilność, wielostabilność, deterministyczny chaos, samoorganizację przestrzenną, fale reaktywności i in.).

Również w organizmach żywych biegną procesy samoorganizacji chemicznej: czasowej (wzorzec wewnętrznego poczucia upływu czasu bazuje być może, na oscylacyjnej reakcji glikolizy, praca serca) i przestrzennej (stały rozwój ciała i jego organów). Tak długo, jak organizm utrzymuje wymianę z zewnętrznym otoczeniem i czerpie z niego reagenty (energię i entropię), może on funkcjonować stabilnie i normalnie. Warunki zachowania samoorganizacji są jednak tak bardzo subtelnej natury, że nie wystarcza to czasami do bezproblemowego funkcjonowania, i z czasem (lawinowo, to także nieliniowość) pojawia się tych zakłóceń coraz więcej...  “chemik nie umiera; chemik tylko przestaje reagować”

Słuchając ulubionych tematów rozmów przypadkowych tzw. “zwykłych ludzi” F w pociągu, można jednak mieć czasem wrażenie, że modelem który nieźle opisuje życie i horyzonty myślowe bardzo wielu moich Rodaków - jest właśnie model butelki i reaktora przepływowego równocześnie... (oczywiście butelki z piwem, sprzężonej z ich układem wydalniczym. I nie ma się co obrażać o taką diagnozę, bo w rozmowie sami wręcz chlubią się oni taką prymitywną postawą, i demonstrują publicznie oba te elementy...)

abstrakcyjni matematycy: teoria katastrof i ratunek w ataku serca - algorytm OGY 

Matematyczna analiza funkcji opisujących przebieg podobnych zjawisk znany jest jako teoria katastrof. Trudno sobie wyobrazić przedmiot równie abstrakcyjny (no, może fizyka kwantowa...). A jednak abstrakcyjni matematycy zajmujący się różnymi sposobami przechodzenia układów przez poszczególne stany, podali propozycję takiego zakłócania pewnego szczególnego stanu (deterministycznego chaosu, czyli stanów uporządkowanych, występujących jednak w nieuporządkowany, przypadkowy sposób) - w rytmiczne oscylacje czasowe. Algorytm ten znany jest jako algorytm OGY (skrót nazwisk matematyków).

W pracy serca następuje czasem groźne zaburzenie znane jako migotanie. Z punktu widzenia naszego opisu, jest to przykład deterministycznego chaosu. Ze stanu tego wyprowadza się za pomocą szokowego zakłócenia impulsem napięcia kilkuset woltów; istnieje pewna szansa, że po takim impulsie za pomocą defibrylatora, układ regulujący pracę serca powróci do regularnych oscylacji. Czasem tak się rzeczywiście dzieje...

Zastosowanie Algorytmu OGY zdaje się dawać szanse na pomyślny wynik terapii o wiele łagodniejszymi środkami.

Zjawiska samoorganizacji w chemii przestały być sensacyjną ciekawostką. Najwyższy czas, aby ich opis wprowadzać do programu studiów z powodu ważności tych procesów, i ich związku z innymi dziedzinami wiedzy. Problemem jest trudność abstrakcyjnego matematycznego opisu tych zjawisk (zarówno dla studentów jak i wielu wykładowców). To opracowanie jest próbą zachęty do innego podejścia: mniej abstrakcyjnego i mniej fachowego, ale chyba bardziej komunikatywnego...

ODSYŁACZE

http://online.redwoods.cc.ca.us/instruct/darnold/DEProj/Sp98/Gabe/intro.htm reakcje oscylacyjne (krótki film)

http://www.ac-nancy-metz.fr/enseign/Physique/video/video2.htm wideo

http://www.faidherbe.org/site/cours/dupuis/jouport.htm

http://www.cheng.cam.ac.uk/~mkraft/pages/teaching/CETIIB-StoMo/WebModule/bz/node4.html  nieco teorii

http://www.wiw.pl/matematyka/diamenty/diamenty_11_02.asp           http://local.wasp.uwa.edu.au/~pbourke/fractals/logistic/ funkcja logistyczna

http://www.mini.pw.edu.pl/MiNIwyklady/fraktale/wstep.html http://www.fractal.art.pl/ http://sprott.physics.wisc.edu/fractals.htm   http://fraktale.aramin.net/    strony z fraktalami (przykładowe)

http://boberov.maszyna.pl/Kippin/127-Granice%20z%B3o%BFono%B6ci/127-06.htm  fragment "Granice złożoności" P.Coveney, R.Highfield
M.Orlik. “Reakcje oscylacyjne, porządek i chaos”. Wyd. WNT, Warszawa 1996.
I.Prigogine, I.Stengers. “Z chaosu ku porządkowi”. Wyd. PIW, Warszawa 1990 (seria “Ą”).
A.L.Kawczyński. “Reakcje chemiczne. Od równowagi przez struktury dyssypatywne do chaosu”. Wyd. WNT, Warszawa 1990.
A.Okniński. “Teoria katastrof w chemii”. Wyd. PWN, Warszawa 1990.
T.Pluciński. “Doświadczenia chemiczne” . Wyd. “Adamantan”, Warszawa 1997, s. 84. [Reakcja Ż-Z-W]
S.Lem. “Cyberiada”, Wyd. VERBA, Chotomów 1990, s. 299. (“Kobyszczę”). [Doświadczenia nad modelami cywilizacji]
 

Tomasz Pluciński
nowy adres:  tomasz.plucinski@ug.edu.pl